A igualdade correta para quaisquer a e b , números reais maiores do que zero, é











 passando pelo seu ponto médio. Chama-se de P a interseção de r com
passando pelo seu ponto médio. Chama-se de P a interseção de r com  . Então, AP + BP vale
. Então, AP + BP vale

A grafite de um lápis tem quinze centímetros de comprimento e dois milímetros de espessura. Dentre os valores abaixo, o que mais se aproxima do número de átomos presentes nessa grafite é
Nota:
1) Assuma que a grafite é um cilindro circular reto, feito de grafita pura. A espessura da grafite é o diâmetro da base do cilindro.
2) Adote os valores aproximados de:
• 2,2 g/cm3 para a densidade da grafita;
• 12 g/mol para a massa molar do carbono;
• 6,0 x 1023 mol-1 para a constante de Avogadro.
Examine o gráfico.

Com base nos dados do gráfico, pode-se afirmar
corretamente que a idade
 , cn = αn+1 - αn e dn = bn+1/bn , definidas para valores inteiros positivos de n, considere as seguintes afirmações:
, cn = αn+1 - αn e dn = bn+1/bn , definidas para valores inteiros positivos de n, considere as seguintes afirmações:No sistema linear  , nas variáveis x , y e z, α e m são constantes reais. É correto afirmar:
, nas variáveis x , y e z, α e m são constantes reais. É correto afirmar:
O sólido da figura é formado pela pirâmide ܵSABCD sobre o
paralelepípedo reto ABCDEFGH. Sabe-se que ܵS pertence à
reta determinada por A e E e que AE = 2cm, AD = 4 cm e AB = 5 cm. A medida do segmento  que faz com que
o volume do sólido seja igual 4/3 do volume da pirâmide SEFGH é
que faz com que
o volume do sólido seja igual 4/3 do volume da pirâmide SEFGH é

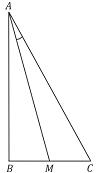
No triângulo retângulo ABC, ilustrado na figura, a
hipotenusa  mede 12cm e o cateto
mede 12cm e o cateto  mede 6 cm. Se M é o ponto médio de
mede 6 cm. Se M é o ponto médio de  , então a tangente do ângulo
, então a tangente do ângulo  é igual a
é igual a

 e
e  números reais com
números reais com 
 Se o sistema de equações, dado em notação matricial,
Se o sistema de equações, dado em notação matricial,
 é igual a
é igual a /3
/3 /6
/6 /6
/6 /3
/3