Questão 5eb24365-97
Prova:USP 2015
Disciplina:Matemática
Assunto:Circunferências, Geometria Analítica
Os pontos A, B e C são colineares, AB = 5, BC = 2 e B está entre A e C. Os pontos C e D pertencem a uma circunferência com centro em A. Traça-se uma reta r perpendicular ao segmento 
passando pelo seu ponto médio. Chama-se de P a interseção de r com 
. Então, AP + BP vale
Os pontos A, B e C são colineares, AB = 5, BC = 2 e B está entre A e C. Os pontos C e D pertencem a uma circunferência com centro em A. Traça-se uma reta r perpendicular ao segmento passando pelo seu ponto médio. Chama-se de P a interseção de r com . Então, AP + BP vale
passando pelo seu ponto médio. Chama-se de P a interseção de r com . Então, AP + BP vale
A
4
B
5
C
6
D
7
E
8
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Fazendo o desenho pedido:
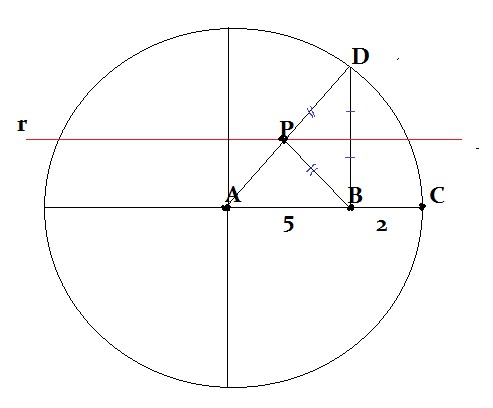
I) Como r é mediatriz de — BD e P ∈ r, tem-se PD = BP
II) O raio da circunferência é AB + BC = 5 + 2 = 7
III) AP + BP = AP + PD = AD = 7, pois AD é raio da circunferência de centro A.
Resposta: Alternativa D.
I) Como r é mediatriz de — BD e P ∈ r, tem-se PD = BP
II) O raio da circunferência é AB + BC = 5 + 2 = 7
III) AP + BP = AP + PD = AD = 7, pois AD é raio da circunferência de centro A.
Resposta: Alternativa D.
