Questão fbc5f51e-3b
Prova:USP 2014
Disciplina:Matemática
Assunto:Geometria Plana, Triângulos
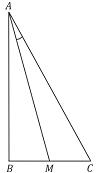
No triângulo retângulo ABC, ilustrado na figura, a
hipotenusa  mede 12cm e o cateto
mede 12cm e o cateto  mede 6 cm. Se M é o ponto médio de
mede 6 cm. Se M é o ponto médio de  , então a tangente do ângulo
, então a tangente do ângulo  é igual a
é igual a
No triângulo retângulo ABC, ilustrado na figura, a
hipotenusa  mede 12cm e o cateto
mede 12cm e o cateto  mede 6 cm. Se M é o ponto médio de
mede 6 cm. Se M é o ponto médio de  , então a tangente do ângulo
, então a tangente do ângulo  é igual a
é igual a

A
√2/7
B
√3/7
C
2/7
D
2√2/7
E
2√3/7
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Aplicando Pitágoras:
AB² + BC² = 12²
AB² + 6² = 12²
AB² = 144 - 36
AB = 6√3 cm
Encontrando "y":
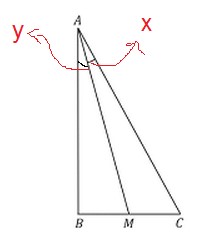
tgy = BM/ AM = 3/6√3 = 1/2√3
Logo:
Tg(x + y) = BC/AB = 6/6√3 = 1/√3
Assim:
tg(x) = tg[(x + y) - y] = [tg(x + y) - tg(y)] / [1+ tg(x + y) . tg(y)]
tg(x) = (1/√3 - 1/2√3) / (1 + 1/√3.1/2√3)
tg(x) = √3/7
Resposta: Alternativa B.
AB² + BC² = 12²
AB² + 6² = 12²
AB² = 144 - 36
AB = 6√3 cm
Encontrando "y":

tgy = BM/ AM = 3/6√3 = 1/2√3
Logo:
Tg(x + y) = BC/AB = 6/6√3 = 1/√3
Assim:
tg(x) = tg[(x + y) - y] = [tg(x + y) - tg(y)] / [1+ tg(x + y) . tg(y)]
tg(x) = (1/√3 - 1/2√3) / (1 + 1/√3.1/2√3)
tg(x) = √3/7
Resposta: Alternativa B.






