Questõesde ENEM sobre Geometria Espacial

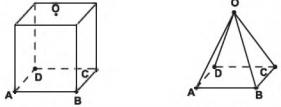
João propôs um desafio a Bruno, seu colega de classe: ele iria descrever um deslocamento pela pirâmide a seguir e Bruno deveria desenhar a projeção desse deslocamento no plano da base da pirâmide.



O deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha reta, do ponto A ao ponto E, a seguir do ponto E ao ponto M, e depois de M a C.

O desenho que Bruno deve fazer é

Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento, como mostra a figura.



O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2.400 cm³ ?

Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.



Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?

Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.


Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de

Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.


Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá

Uma empresa vende tanques de combustíveis de formato cilíndrico, em três tamanhos, com medidas indicadas nas figuras. O preço do tanque é diretamente proporcional à medida da área da superfície lateral do tanque. O dono de um posto de combustível deseja encomendar um tanque com menor custo por metro cúbico de capacidade de armazenamento.



Qual dos tanques deverá ser escolhido pelo dono do posto? (Considere π ≅ 3)

Para construir uma manilha de esgoto, um cilindro com 2 m de diâmetro e 4 m de altura (de espessura desprezível), foi envolvido homogeneamente por uma camada de concreto, contendo 20 cm de espessura.

Supondo que cada metro cúbico de concreto custe R$ 10,00 e tomando 3,1 como valor aproximado de π então o preço dessa manilha é igual a

No manejo sustentável de florestas, é preciso muitas vezes obter o volume da tora que pode ser obtida a partir de uma árvore. Para isso, existe um método prático, em que se mede a circunferência da árvore à altura do peito de um homem (1,30m), conforme indicado na figura. A essa medida denomina-se “rodo" da árvore. O quadro a seguir indica a fórmula para se cubar, ou seja, obter o volume da tora em m³ a partir da medida do rodo e da altura da árvore.


Um técnico em manejo florestal recebeu a missão de cubar, abater e transportar cinco toras de madeira, de duas espécies diferentes, sendo

3 toras da espécie I, com 3 m de rodo, 12 m de comprimento e densidade 0,77 toneladas/m³ ;

2 toras da espécie II, com 4m de rodo, 10m de comprimento e densidade 0,78 toneladas/m³ .

Após realizar seus cálculos, o técnico solicitou que enviassem caminhões para transportar uma carga de, aproximadamente,

Uma metalúrgica recebeu uma encomenda para fabricar, em grande quantidade, uma peça com o formato de um prisma reto com base triangular, cujas dimensões da base são 6 cm, 8 cm e 10 cm e cuja altura é 10 cm. Tal peça deve ser vazada de tal maneira que a perfuração na forma de um cilindro circular reto seja tangente às suas faces laterais, conforme mostra a figura.


O raio da perfuração da peça é igual a

Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.


O volume de madeira utilizado na confecção desse objeto foi de

Considerando que nenhum dos recipientes tenha tampa, qual das figuras a seguir representa uma planificação para o bebedouro 3?

Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a

A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com as dimensões indicadas na figura que segue.


O produto das três dimensões indicadas na peça resultaria na medida da grandeza

Uma indústria fabrica brindes promocionais em forma de pirâmide. A pirâmide é obtida a partir de quatro cortes em um sólido que tem a forma de um cubo. No esquema, estão indicados o sólido original (cubo) e a pirâmide obtida a partir dele.



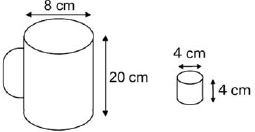
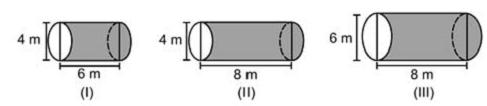
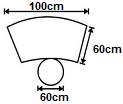
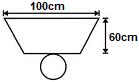
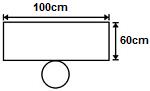
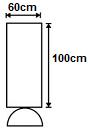
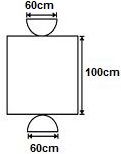
Os pontos A, B, C, D e O do cubo e da pirâmide são os mesmos. O ponto O é central na face superior do cubo. Os quatro cortes saem de O em direção às arestas , nessa ordem. Após os cortes, são descartados quatro sólidos.

Os formatos dos sólidos descartados são

A resistência das vigas de dado comprimento é diretamente proporcional à largura (b) e ao quadrado da altura (d), conforme a figura. A constante de proporcionalidade k varia de acordo com o material utilizado na sua construção.



Considerando-se S como a resistência, a representação algébrica que exprime essa relação é

É possível usar água ou comida para atrair as aves e observá-las. Muitas pessoas costumam usar água com açúcar, por exemplo, para atrair beija-flores. Mas é importante saber que, na hora de fazer a mistura, você deve sempre usar uma parte de açúcar para cinco partes de água. Além disso, em dias quentes, precisa trocar a água de duas a três vezes, pois com o calor ela pode fermentar e, se for ingerida pela ave, pode deixá- la doente. O excesso de açúcar, ao cristalizar, também pode manter o bico da ave fechado, impedindo-a de se alimentar. Isso pode até matá-la.
Ciência Hoje das Criança s. FNDE; Instituto Ciência Hoje, ano 19, n. 166, mar. 1996.

Pretende-se encher completamente um copo com a mistura para atrair beija-flores. O copo tem formato cilíndrico, e suas medidas são 10 cm de altura e 4 cm de diâmetro. A quantidade de água que deve ser utilizada na mistura é cerca de (utilize π = 3)

A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.



Esta figura é uma representação de uma superfície de revolução chamada de

Supondo-se que o custo da vela seja diretamente proporcional ao volume de parafina empregado, o custo da vela do tipo I, em relação ao custo da vela do tipo II, será

Os três recipientes da figura têm formas diferentes, mas a mesma altura e o mesmo diâmetro da boca. Neles são colocados líquido até a metade de sua altura, conforme indicado nas figuras. Representando por o volume de líquido em cada um dos recipientes, tem-se

Um artesão construiu peças de artesanato interceptando uma pirâmide de base quadrada com um plano. Após fazer um estudo das diferentes peças que poderia obter, ele concluiu que uma delas poderia ter uma das faces pentagonal.

Qual dos argumentos a seguir justifica a conclusão do artesão?