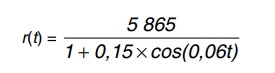Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função
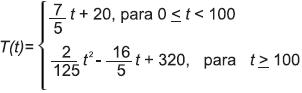
em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 °C e retirada quando a temperatura for 200 °C.
O tempo de permanência dessa peça no forno é, em minutos, igual a
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função
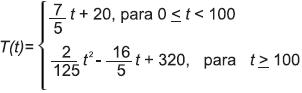
em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 °C e retirada quando a temperatura for 200 °C.
O tempo de permanência dessa peça no forno é, em minutos, igual a


 R.
R. R.
R. R.
R.