Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por
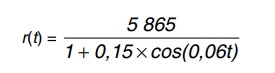
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por
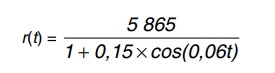
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
Gabarito comentado
Esta
questão requer que o candidato demonstre conceitos básicos de Trigonometria,
especificamente sobre os valores máximo e mínimo de seno e cosseno.
Sendo assim, ressalta-se que tanto o seno como o cosseno de qualquer número variam de -1 até +1. Assim, de acordo com o enunciado e independente do valor de t, tem-se:
-
1 ≤ cos (0,06t) ≤ + 1 ,
onde + 1 e - 1 são os valores máximo e mínimo de cos(0,06t) e consequentemente ao
serem substituídos na função r(t), maximizam ou minimizam a mesma.
Finalizando, tem-se:
a) substituindo cos(0,06t) por -1:
r = 5865 / [1 + 0,15 x (-1)] = 6900
b)
substituindo cos(0,06t) por +1:
r = 5865 / [1 + 0,15 x 1] = 5100
Assim, S = 6900 + 5100 = 12000
km
Resposta
B.






