Questão c3d48e6d-bb
Prova:ENEM 2010
Disciplina:Matemática
Assunto:Funções, Função de 1º Grau, Função de 2º Grau
Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função
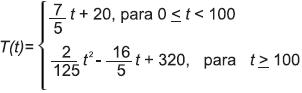
em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 °C e retirada quando a temperatura for 200 °C.
O tempo de permanência dessa peça no forno é, em minutos, igual a
Nos processos industriais, como na indústria de cerâmica, é necessário o uso de fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo de elevação dessa temperatura deve ser controlado, para garantir a qualidade do produto final e a economia no processo.
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função
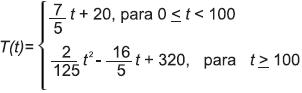
em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 °C e retirada quando a temperatura for 200 °C.
O tempo de permanência dessa peça no forno é, em minutos, igual a
Em uma indústria de cerâmica, o forno é programado para elevar a temperatura ao longo do tempo de acordo com a função
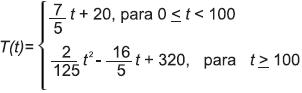
em que T é o valor da temperatura atingida pelo forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura for 48 °C e retirada quando a temperatura for 200 °C.
O tempo de permanência dessa peça no forno é, em minutos, igual a
A
100.
B
108.
C
128.
D
130.
E
150.
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Teremos que calcular em duas etapas, no intervalo 0 ≤ t ≤ 100, a temperatura varia da seguinte maneira:
T(0) = (7/5).0 + 20 = 20°C
T(100) = (7/5).100 + 20 = 160°C
Se a peça foi colocada no forno a 48°C, então:
i)48 = (7/5)t + 20
48 - 20 =(7/5)t
t = 28 x (5/7)
t = 20 min
A peça foi retirada quando a temperatura a 200 °C, assim, utilizamos a segunda equação (quadrática):
ii)
200 = (2/125)t² - (16/5)t + 320
(2/125)t² - (16/5)t + 120 = 0
Multiplicando tudo por 125:
2t² - 400t + 15.000 = 0
Agora dividindo-se tudo por 2:
t² - 200t + 7.500 = 0
Resolvendo pela Fórmula de Bhaskara, encontraremos duas raízes reais:
t1 =150 min e
t2 = 50 min < 100 min, como visto acima, não convém.
Como a peça entrou com após 20 minutos do forno ligado e saiu 150 minutos depois, ela permaneceu no forno 150 - 20 = 130 min.
Resposta: Alternativa D.






