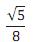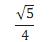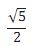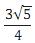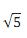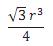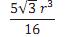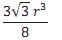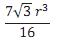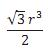Questõesde USP sobre Matemática
Foram encontradas 141 questões
8a4120c8-12
USP 2011 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales
Na figura, tem-se 
, paralelo a 
paralelo a 
Na figura, tem-se , paralelo a paralelo a
, paralelo a paralelo a A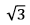
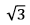
B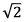
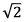
C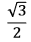
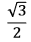
D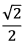
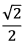
E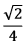
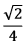
9b6f1ef2-12
USP 2011 - Matemática - Probabilidade
Francisco deve elaborar uma pesquisa sobre dois artrópodes distintos. Eles serão selecionados, ao acaso, da seguinte relação: aranha, besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, carrapato, escorpião e gafanhoto.
Qual é a probabilidade de que ambos os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
Francisco deve elaborar uma pesquisa sobre dois artrópodes distintos. Eles serão selecionados, ao acaso, da seguinte relação: aranha, besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, carrapato, escorpião e gafanhoto.
Qual é a probabilidade de que ambos os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
Qual é a probabilidade de que ambos os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
A
49/144
B
14/33
C
7/22
D
5/22
E
15/144
989f4cf7-12
USP 2011 - Matemática - Funções, Equações Exponenciais
Uma substância radioativa sofre desintegração ao
Uma substância radioativa sofre desintegração ao
A
10%
B
5%
C
4%
D
3%
E
2%
95823eb7-12
USP 2011 - Matemática - Geometria Espacial, Poliedros
Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a
Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a
A
B
C
D
E
92b32c36-12
USP 2011 - Matemática - Probabilidade
Considere todos os pares ordenados de números naturais (a,b), em que 11 ≤ α ≤ 22 e 43 ≤ b ≤ 51.
Cada um desses pares ordenados está escrito em um cartão diferente. Sorteando-se um desses cartões ao acaso, qual é a probabilidade de que se obtenha um par ordenado ( a, b ) de tal forma que a fração a/b seja irredutível e com denominador par?
Considere todos os pares ordenados de números naturais (a,b), em que 11 ≤ α ≤ 22 e 43 ≤ b ≤ 51.
Cada um desses pares ordenados está escrito em um cartão diferente. Sorteando-se um desses cartões ao acaso, qual é a probabilidade de que se obtenha um par ordenado ( a, b ) de tal forma que a fração a/b seja irredutível e com denominador par?
A
7/27
B
13/54
C
6/27
D
11/54
E
5/27
8fe067a0-12
USP 2011 - Matemática - Pontos e Retas, Geometria Analítica, Geometria Plana
No plano cartesiano 0xy, a circunferência C é tangente ao eixo 0x no ponto de abscissa 5 e contém o ponto ( 1,2 ) . Nessas condições, o raio de C vale
No plano cartesiano 0xy, a circunferência C é tangente ao eixo 0x no ponto de abscissa 5 e contém o ponto ( 1,2 ) . Nessas condições, o raio de C vale
A
√5
B
2√5
C
5
D
3√5
E
10
87707a65-12
USP 2011 - Matemática - Progressão Aritmética - PA, Geometria Plana, Progressões
Em um plano, é dado um polígono convexo de seis lados, cujas medidas dos ângulos internos, dispostas em ordem crescente, formam uma progressão aritmética. A medida do maior ângulo é igual a 11 vezes a medida do menor. A soma das medidas dos quatro menores ângulos internos desse polígono, em graus, é igual a
Em um plano, é dado um polígono convexo de seis lados, cujas medidas dos ângulos internos, dispostas em ordem crescente, formam uma progressão aritmética. A medida do maior ângulo é igual a 11 vezes a medida do menor. A soma das medidas dos quatro menores ângulos internos desse polígono, em graus, é igual a
A
315
B
320
C
325
D
330
E
335
84a07225-12
USP 2011 - Matemática - Funções, Função de 1º Grau
Considere a função
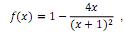
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
Considere a função
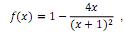
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
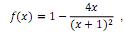
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
A
-1
B
1
C
x +1
D
x 2 +1
E
( x - 1 ) 2
81d17bd8-12
USP 2011 - Matemática - Trigonometria, Funções, Logaritmos
O número real x, com 0 < x < π , satisfaz a equação
O número real x, com 0 < x < π , satisfaz a equação
A
1/3
B
2/3
C
7/9
D
8/9
E
10/9
7f01215c-12
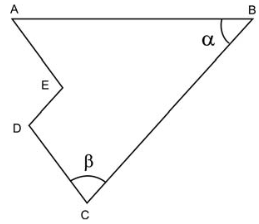
USP 2011 - Matemática - Geometria Plana
O segmento 
é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de 
de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento 
é igual a
O segmento é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento é igual a
é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento é igual a A
√2
B
2 √ 2
C
3√ 2
D
√3
E
2 √3
7c3298b7-12
USP 2011 - Matemática - Aritmética e Problemas
Em uma festa com n pessoas, em um dado instante, 31 mulheres se retiraram e restaram convidados na razão de 2 homens para cada mulher. Um pouco mais tarde, 55 homens se retiraram e restaram, a seguir, convidados na razão de 3 mulheres para cada homem. O número n de pessoas presentes inicialmente na festa era igua a
Em uma festa com n pessoas, em um dado instante, 31 mulheres se retiraram e restaram convidados na razão de 2 homens para cada mulher. Um pouco mais tarde, 55 homens se retiraram e restaram, a seguir, convidados na razão de 3 mulheres para cada homem. O número n de pessoas presentes inicialmente na festa era igua a
A
100
B
105
C
115
D
130
E
135
625be399-fc
USP 2010 - Matemática - Probabilidade
Um dado cúbico, não viciado, com faces numeradas de 1 a 6, é lançado três vezes. Em cada lançamento, anota-se o número obtido na face superior do dado, formando-se uma sequência (a, b, c ). Qual é a probabilidade de que b seja sucessor de a ou que c seja sucessor de b ?
Um dado cúbico, não viciado, com faces numeradas de 1 a 6, é lançado três vezes. Em cada lançamento, anota-se o número obtido na face superior do dado, formando-se uma sequência (a, b, c ). Qual é a probabilidade de que b seja sucessor de a ou que c seja sucessor de b ?
A
B
C
D
E
6091bfef-fc
USP 2010 - Matemática - Seno, Cosseno e Tangente, Trigonometria
Sejam 
números reais positivos tais que 
Sabendo-se que 
o valor de 
é igual a
Sejam números reais positivos tais que Sabendo-se que o valor de é igual a
números reais positivos tais que Sabendo-se que o valor de é igual aA
B
C
D
E
5fae152c-fc
USP 2010 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos
Na figura, o triângulo A B C é equilátero de lado 1, e A C D E , A F G B e B H I C são quadrados. A área do poligono D E F G H I vale
Na figura, o triângulo A B C é equilátero de lado 1, e A C D E , A F G B e B H I C são quadrados. A área do poligono D E F G H I vale
A
B
C
D
E
5ecb8666-fc
USP 2010 - Matemática - Progressão Aritmética - PA, Progressões
Seja 
tal que a sequência 
forme, nessa ordem, uma progressão aritmética. Então, 
é igual a
Seja tal que a sequência forme, nessa ordem, uma progressão aritmética. Então, é igual a
tal que a sequência forme, nessa ordem, uma progressão aritmética. Então, é igual aA
B
C
D
E
5de7e18f-fc
USP 2010 - Matemática - Quadriláteros, Geometria Plana
No losango A B C D de lado 1, representado na figura, tem - se que M é o ponto médio de
, N é o ponto médio de 
e 
. Então, DM é igual a
No losango A B C D de lado 1, representado na figura, tem - se que M é o ponto médio de, N é o ponto médio de e . Então, DM é igual a
, N é o ponto médio de e . Então, DM é igual aA
B
C
D
E
