Questão 84a07225-12
Prova:USP 2011
Disciplina:Matemática
Assunto:Funções, Função de 1º Grau
Considere a função
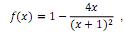
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
Considere a função
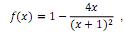
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
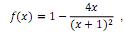
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
A
-1
B
1
C
x +1
D
x 2 +1
E
( x - 1 ) 2
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
De acordo com enunciado, x ≠ 1 e x ≠ - 1, logo:
f(x)=1-4x/(x+1)2 =(x-1)2/(x+1)2 e analogamente,f(-x)=1+4x/(x-1)2 =(x+1)²/(x-1)²
Multiplicando o resultado de f(x).f(-x) temos (x-1)2/(x+1)2 . (x+1)²/(x-1)²=1.
Logo, alternativa correta letra B.






