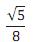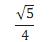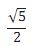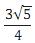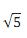Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado 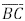 e N o ponto médio do lado
e N o ponto médio do lado 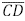 . Os segmentos
. Os segmentos 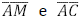 interceptam o segmento
interceptam o segmento 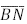 nos pontos E e F, respectivamente.
nos pontos E e F, respectivamente.

A área do triângulo AEF é igual a
Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado 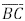 e N o ponto médio do lado
e N o ponto médio do lado 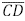 . Os segmentos
. Os segmentos 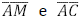 interceptam o segmento
interceptam o segmento 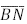 nos pontos E e F, respectivamente.
nos pontos E e F, respectivamente.

A área do triângulo AEF é igual a
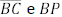 = 1. Os pontos R, S e T pertencem aos lados
= 1. Os pontos R, S e T pertencem aos lados 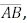
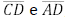 , respectivamente. O segmento
, respectivamente. O segmento 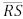 é paralelo a
é paralelo a 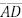 e intercepta
e intercepta 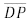 no ponto Q. O segmento
no ponto Q. O segmento 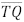 é paralelo a
é paralelo a 

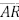 , o maior valor da soma das áreas do retângulo
, o maior valor da soma das áreas do retângulo 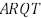 , do triângulo CQP e do triângulo DQS, para x variando no intervalo aberto ] 0,3[, é
, do triângulo CQP e do triângulo DQS, para x variando no intervalo aberto ] 0,3[, é
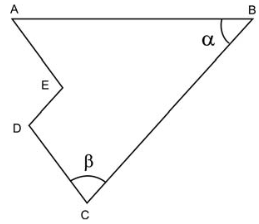
 e
e  são retos, AB = AD = 1, BC = CD = 2 e
são retos, AB = AD = 1, BC = CD = 2 e  é uma diagonal.O cosseno do ângulo
é uma diagonal.O cosseno do ângulo  vale
vale , passa o plano α paralelo às arestas
, passa o plano α paralelo às arestas  e
e  . Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
. Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
 mede 12
mede 12 mede 6
mede 6  , então a tangente do ângulo
, então a tangente do ângulo  é igual a
é igual a 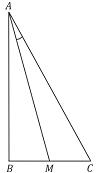
 são segmentos de reta, o ponto G está no segmento
são segmentos de reta, o ponto G está no segmento  o ponto E está no segmento
o ponto E está no segmento  é um retângulo e
é um retângulo e  é um trapézio. Se AF = 15, AG = 12, AB = 6, CD = 3 e DF = 5
é um trapézio. Se AF = 15, AG = 12, AB = 6, CD = 3 e DF = 5 indicam valores em centímentros no mapa real, então a área da APP é
indicam valores em centímentros no mapa real, então a área da APP é








 , paralelo a
, paralelo a  paralelo a
paralelo a 
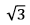
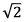
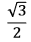
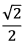
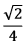
 é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de
é lado de um hexágono regular de área √3. O ponto P pertence à mediatriz de  de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento
de tal modo que a área do triângulo PAB vale √2. Então, a distância de P ao segmento  é igual a
é igual a  , N é o ponto médio de
, N é o ponto médio de  e
e  . Então, DM é igual a
. Então, DM é igual a