Questão 5ee7b4d0-97
Prova:USP 2015
Disciplina:Matemática
Assunto:Quadriláteros, Geometria Plana
Cada aresta do tetraedro regular ABCD mede 10. Por um ponto P na aresta  , passa o plano α paralelo às arestas
, passa o plano α paralelo às arestas  e
e  . Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
. Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
Cada aresta do tetraedro regular ABCD mede 10. Por um ponto P na aresta  , passa o plano α paralelo às arestas
, passa o plano α paralelo às arestas  e
e  . Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
. Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
 , passa o plano α paralelo às arestas
, passa o plano α paralelo às arestas  e
e  . Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
. Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
A
21
B
21√2 / 2
C
30
D
30/2
E
30√3 / 2
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Desenhando de acordo com o enunciado:
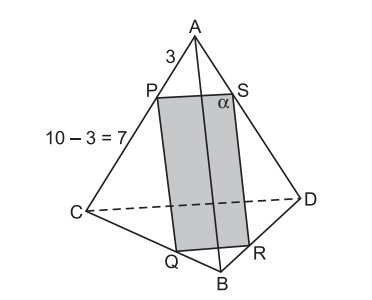
Assim:
7 x 3 = 21
Resposta: Alternativa A.

Assim:
Sabemos que α é paralelo às arestas AB e CD, as interseções de α com as faces ABC e ABD são paralelas a AB e as interseções de α com as faces ACD e BCD são paralelas a CD.
Assim, por simetria, AB | CD, o quadrilátero PQRS determinado pelas interseções de α com as arestas do tetraedro é um retângulo.
Como PQ // AB e PS // CD, os triângulos CPQ e APS são equiláteros de lados PC = 10 – 3 = 7 e AP = 3, respectivamente. Então, a área de PQRS é:7 x 3 = 21
Resposta: Alternativa A.






