Questõesde ENEM sobre Geometria Plana

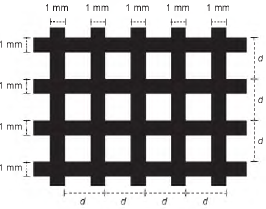
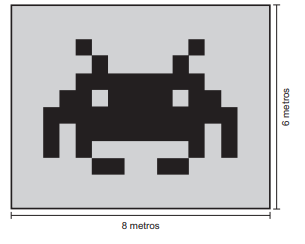
Pretende-se construir um mosaico com o formato de um triângulo retângulo, dispondo-se de três peças, sendo duas delas triângulos retângulos congruentes e a terceira um triângulo isósceles. Afigura apresenta cinco mosaicos formados por três peças.

Na figura, o mosaico que tem as características daquele que se pretende construir é o

Um grupo de escoteiros mirins, numa atividade no parque da cidade onde moram, montou uma barraca conforme a foto da Figura 1. A Figura 2 mostra o esquema da estrutura dessa barraca, em forma de um prisma reto, em que foram usadas hastes metálicas.

Após a armação das hastes, um dos escoteiros observou um inseto deslocar-se sobre elas, partindo do vértice A em direção ao vértice B, deste em direção ao vértice E e, finalmente, fez o trajeto do vértice E ao C. Considere que todos esses deslocamentos foram feitos pelo caminho de menor distância entre os pontos.

A projeção do deslocamento do inseto no plano que contém a base ABCD é dada por

Dispondo de um grande terreno, uma empresa de entretenimento pretende construir um espaço retangular para shows e eventos, conforme a figura.

A área para o público será cercada com dois tipos de materiais:

• nos lados paralelos ao palco será usada uma tela do tipo A, mais resistente, cujo valor do metro linear é R$ 20,00;

• nos outros dois lados será usada uma tela do tipo B, comum, cujo metro linear custa R$ 5,00.

A empresa dispõe de R$ 5 000,00 para comprar todas as telas, mas quer fazer de tal maneira que obtenha a maior área possível para o público.

A quantidade de cada tipo de tela que a empresa deve comprar é

Um terreno retangular de lados cujas medidas, em metro, são x e y será cercado para a construção de um parque de diversões. Um dos lados do terreno encontra-se às margens de um rio. Observe a figura.

Para cercar todo o terreno, o proprietário gastará R$ 7 500,00. O material da cerca custa R$ 4,00 por metro para os lados do terreno paralelos ao rio, e R$ 2,00 por metro para os demais lados.

Nessas condições, as dimensões do terreno e o custo total do material podem ser relacionados pela equação

      Um agricultor vive da plantação de morangos que são vendidos para uma cooperativa. A cooperativa faz um contrato de compra e venda no qual o produtor informa a área plantada.

      Para permitir o crescimento adequado das plantas, as mudas de morango são plantadas no centro de uma área retangular, de 10cm por 20 cm, como mostra a figura. 

      Atualmente, sua plantação de morangos ocupa uma área de 10 000 m2, mas a cooperativa quer que ele aumente sua produção. Para isso, o agricultor deverá aumentar a área plantada em 20%, mantendo o mesmo padrão de plantio.

O aumento (em unidade) no número de mudas de morango em sua plantação deve ser de 

O proprietário de um restaurante deseja comprar um tampo de vidro retangular para a base de uma mesa, como ilustra a figura.

Sabe-se que a base da mesa, considerando a borda externa, tem a forma de um retângulo, cujos lados medem AC = 105 cm e AB = 120 cm.

Na loja onde será feita a compra do tampo, existem cinco tipos de opções de tampos, de diferentes dimensões, e todos com a mesma espessura, sendo:

Tipo 1: 110 cm x 125 cm

Tipo 2: 115 cm x 125 cm

Tipo 3: 115 cm x 130 cm

Tipo 4: 120 cm x 130 cm

Tipo 5: 120 cm x 135 cm

O proprietário avalia, para comodidade dos usuários, que se deve escolher o tampo de menor área possível que satisfaça a condição: ao colocar o tampo sobre a base, de cada lado da borda externa da base da mesa, deve sobrar uma região, correspondendo a uma moldura em vidro, limitada por um mínimo de 4 cm e máximo de 8 cm fora da base da mesa, de cada lado.

Segundo as condições anteriores, qual é o tipo de tampo de vidro que o proprietário avaliou que deve ser escolhido?

      É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada.

Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico?

Em uma cidade será construída uma galeria subterrânea que receberá uma rede de canos para o transporte de água de uma fonte (F) até o reservatório de um novo bairro (B).

Após avaliações, foram apresentados dois projetos para o trajeto de construção da galeria: um segmento de reta que atravessaria outros bairros ou uma semicircunferência que contornaria esses bairros, conforme ilustrado no sistema de coordenadas xOy da figura, em que a unidade de medida nos eixos é o quilômetro.

Estudos de viabilidade técnica mostraram que, pelas características do solo, a construção de 1 m de galeria via segmento de reta demora 1,0 h, enquanto que 1 m de construção de galeria via semicircunferência demora 0,6 h. Há urgência em disponibilizar água para esse bairro.

Use 3 como aproximação para π e 1,4 como aproximação para √2.

O menor tempo possível, em hora, para conclusão da construção da galeria, para atender às necessidades de água do bairro, é de

Um senhor, pai de dois filhos, deseja comprar dois terrenos, com áreas de mesma medida, um para cada filho. Um dos terrenos visitados já está demarcado e, embora não tenha um formato convencional (como se observa na Figura B), agradou ao filho mais velho e, por isso, foi comprado. O filho mais novo possui um projeto arquitetônico de uma casa que quer construir, mas, para isso, precisa de um terreno na forma retangular (como mostrado na Figura A) cujo comprimento seja 7 m maior do que a largura.

Para satisfazer o filho mais novo, esse senhor precisa encontrar um terreno retangular cujas medidas, em metro, do comprimento e da largura sejam iguais, respectivamente, a

Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.

A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.

Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas

O Esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.