Questão 96cd9227-7f
Prova:ENEM 2015
Disciplina:Matemática
Assunto:Áreas e Perímetros, Geometria Plana
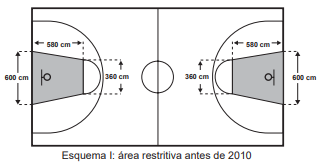
O Esquema I mostra a configuração de uma quadra
de basquete. Os trapézios em cinza, chamados de
garrafões, correspondem a áreas restritivas.
Visando atender as orientações do Comitê Central da
Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
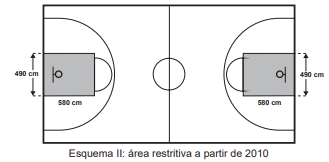
Após executadas as modificações previstas, houve
uma alteração na área ocupada por cada garrafão, que
corresponde a um(a)
O Esquema I mostra a configuração de uma quadra
de basquete. Os trapézios em cinza, chamados de
garrafões, correspondem a áreas restritivas.

Visando atender as orientações do Comitê Central da
Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.

Após executadas as modificações previstas, houve
uma alteração na área ocupada por cada garrafão, que
corresponde a um(a)
A
aumento de 5 800 cm2 .
B
aumento de 75 400 cm2.
C
aumento de 214 600 cm2.
D
diminuição de 63 800 cm2.
E
diminuição de 272 600 cm2.
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Calculando-se a área ado trapézio, temos:
At = (B + b)H / 2
At = (600 + 360)580 / 2
At = 278.400 cm²
Calculando agora a área do retângulo:
Ar = 580 x 490 = 284.200 cm²
Calculando a diferença entre as áreas:
Ar - At = 284.200 - 278.400 = 5.800 cm²
Resposta: Alternativa A.
At = (B + b)H / 2
At = (600 + 360)580 / 2
At = 278.400 cm²
Calculando agora a área do retângulo:
Ar = 580 x 490 = 284.200 cm²
Calculando a diferença entre as áreas:
Ar - At = 284.200 - 278.400 = 5.800 cm²
Resposta: Alternativa A.






