Uma fórmula para calcular o Índice de Massa
Corporal (IMC) foi publicada pelo Departamento de
Nutrição da Universidade de São Paulo. O estudo
propõe uma equação capaz de identificar os falsos
magros que, apesar de exibirem uma silhueta esguia,
apresentam altos níveis de gordura, e os falsos gordos,
que têm um IMC alto em decorrência de ganho de
massa muscular, e não de gordura.
A equação considera a massa do indivíduo, além do
peso e da estatura. A fórmula é expressa pela soma do
triplo da massa (M), em quilograma, com o quádruplo do
percentual de gordura (G), tudo dividido pela altura (H),
em centímetro.
Disponível em: http://drauziovarella.com.br. Acesso em: 27 nov. 2012 (adaptado).
A expressão algébrica que representa a nova maneira de
calcular o IMC é dada por
Uma fórmula para calcular o Índice de Massa Corporal (IMC) foi publicada pelo Departamento de Nutrição da Universidade de São Paulo. O estudo propõe uma equação capaz de identificar os falsos magros que, apesar de exibirem uma silhueta esguia, apresentam altos níveis de gordura, e os falsos gordos, que têm um IMC alto em decorrência de ganho de massa muscular, e não de gordura.
A equação considera a massa do indivíduo, além do peso e da estatura. A fórmula é expressa pela soma do triplo da massa (M), em quilograma, com o quádruplo do percentual de gordura (G), tudo dividido pela altura (H), em centímetro.
Disponível em: http://drauziovarella.com.br. Acesso em: 27 nov. 2012 (adaptado).
A expressão algébrica que representa a nova maneira de
calcular o IMC é dada por




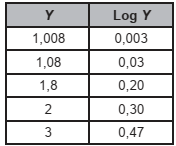


 , a equação
algébrica x
, a equação
algébrica x



