Questõesde ENEM sobre Trigonometria

Início Todas as questões

Foram encontradas 10 questões

ENEM 2021 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é

Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo

, em que A > 0 é a amplitude de deslocamento máximo e ω é a frequência, que se relaciona com o período T pela fórmula

.

Considere a ausência de quaisquer forças dissipativas.

A

-3 cos (2t)

B

-3 sen (2t)

C

3 cos (2t)

D

-6 cos (2t)

E

6 sen (2t)

ENEM 2021 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = ± A cos (ωt) ou P(t) = ± A sen (ωt), em que A > 0 é a amplitude de deslocamento máximo e ω é a frequência, que se relaciona com o período T pela fórmula ω = 2π/T.

Considere a ausência de quaisquer forças dissipativas.

A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é

A

– 3 cos (2t)

B

– 3 sen (2t)

C

3 cos (2t)

D

– 6 cos (2t)

E

6 sen (2t)

ENEM 2018 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:

A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t.

Após duas voltas completas, f em o seguinte gráfico:

A expressão da função altura é dada por

A

f(t) = 80sen(t) + 88

B

f(t) = 80cos(t) + 88

C

f(t) = 88 cos(t)+168

D

f(t) = 168sen(t) + 88 cos(t)

E

f(t) = 88 sen(t)+ 168cos(t)

ENEM 2014 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Uma pessoa usa um programa de computador que descreve o desenho da onda sonora correspondente a um som escolhido. A equação da onda é dada, num sistema de coordenadas cartesianas, por y = a . sen[b(x + c)], em que os parâmetros a, b, c são positivos. O programa permite ao usuário provocar mudanças no som, ao fazer alterações nos valores desses parâmetros. A pessoa deseja tornar o som mais agudo e, para isso, deve diminuir o período da onda.

O(s) único(s) parâmetro(s) que necessita(m) ser alterado(s) é(são)

A

a.

B

b.

C

c.

D

a e b.

E

b e c.

ENEM 2015 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

Um técnico precisa consertar o termostato do aparelho de ar-condicionado de um escritório, que está desregulado. A temperatura T, em graus Celsius, no escritório, varia de acordo com a função T (h) = A + B sen, sendo h o tempo, medido em horas, a partir da meia-noite (0 ≤ h ≤ 24) e A e B os parâmetros que o técnico precisa regular. Os funcionários do escritório pediram que a temperatura máxima fosse 26°C, a mínima 18°C, e que durante a tarde a temperatura fosse menor do que durante a manhã.

Quais devem ser os valores de A e de B para que o pedido dos funcionários seja atendido?

A

A = 18 e B = 8

B

A = 22 e B = - 4

C

A = 22 e B = 4

D

A = 26 e B = - 8

E

A = 26 e B = 8

ENEM 2017 - Matemática - Trigonometria, Círculo Trigonométrico

Para decorar uma mesa de festa infantil, um chefe de cozinha usará um melão esférico com diâmetro medindo 10 cm, o qual servirá de suporte para espetar diversos doces. Ele irá retirar uma calota esférica do melão, conforme ilustra a figura, e, para garantir a estabilidade deste suporte, dificultando que o melão role sobre a mesa, o chefe fará o corte de modo que o raio rda seção circular de corte seja de pelo menos 3 cm. Por outro lado, o chefe desejará dispor da maior área possível da região em que serão afixados os doces.

Para atingir todos os seus objetivos, o chefe deverá cortar a calota do melão numa altura h, em centímetro, igual a

A

B

10 - √91

C

1

D

4

E

5

ENEM 2017 - Matemática - Trigonometria, Funções, Funções Trigonométricas e Funções Trigonométricas Inversas

Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função do tipo P(t) = A + Bcos(kt) em que A, B e K são constantes reais positivas e t representa a variável tempo, medida em segundo. Considere que um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões máximas.

Ao analisar um caso específico, o cientista obteve os dados:

A função P(t) obtida, por este cientista, ao analisar o caso específico foi

A

P(t) = 99 + 2 1 cos(3πt)

B

P(t) = 78 + 42cos(3πt)

C

P(t) = 99 + 21 cos(2πt)

D

P(t) = 99 + 21 cos(t)

E

P(t) = 78 + 42cos(t)

ENEM 2015 - Matemática - Trigonometria

Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra.

A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de um certo produto sazonal pode ser descrito pela função P(x) = 8 + 5cos onde x representa o mês do ano,sendo x = 1 associado ao mês de janeiro x = 2 ao mês de fevereiro e assim sucessivamente, até x= 12 associado ao mês de dezembro.

Disponivel em : www.ibge.gov.br em 2 ago.2012 (adaptado)

Na safra.o mês de produção máxima desse produto é

A

janeiro

B

abril

C

junho

D

julho

E

outubro

ENEM 2014 - Matemática - Trigonometria

Uma criança deseja criar triângulos utilizando palitos de fósforo de mesmo comprimento. Cada triângulo será construído com exatamente 17 palitos e pelo menos um dos lados do triângulo deve ter o comprimento de exatamente 6 palitos. A figura ilustra um triângulo construído com essas características.

A quantidade máxima de triângulos não congruentes dois a dois que podem ser construídos é

A

3.

B

5.

C

6.

D

8.

E

10.

ENEM 2010 - Matemática - Trigonometria

Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por

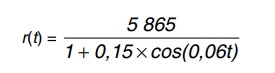
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.

O cientista deveria concluir que, periodicamente, S atinge o valor de

A

12 765 km.

B

12 000 km.

C

11 730 km.

D

10 965 km.

E

5 865 km.