Questão 970b0537-7f
Prova:ENEM 2015
Disciplina:Matemática
Assunto:Funções, Logaritmos
Um engenheiro projetou um automóvel cujos vidros
das portas dianteiras foram desenhados de forma que
suas bordas superiores fossem representadas pela curva
de equação y = log (x), conforme a figura.

A forma do vidro foi concebida de modo que o eixo
x sempre divida ao meio a altura h do vidro e a base
do vidro seja paralela ao eixo x. Obedecendo a essas
condições, o engenheiro determinou uma expressão que
fornece a altura h do vidro em função da medida n de sua
base, em metros.
A expressão algébrica que determina a altura do vidro é
Um engenheiro projetou um automóvel cujos vidros
das portas dianteiras foram desenhados de forma que
suas bordas superiores fossem representadas pela curva
de equação y = log (x), conforme a figura.

A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a base do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro determinou uma expressão que fornece a altura h do vidro em função da medida n de sua base, em metros.
A expressão algébrica que determina a altura do vidro é

A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a base do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro determinou uma expressão que fornece a altura h do vidro em função da medida n de sua base, em metros.
A expressão algébrica que determina a altura do vidro é
A

B

C

D

E

Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Desenhando o gráfico abaixo:
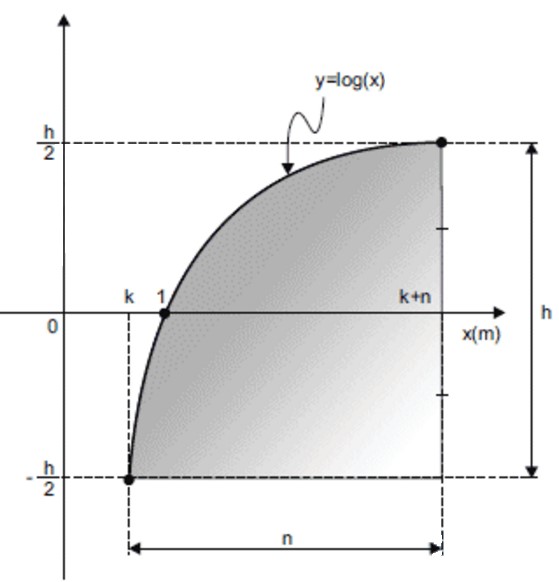
Temos que:
log(k + n) = h/2
log k = -h/2
Assim:
2 log(k + n) = h (1)
-2 log k = h
Então
h = h
2 log(k + n) = -2log k
log(k + n) = - log k
log(k + n) + log k = 0
log[(k + n)k] = 0
elog[(k + n)k] = e0
[(k + n)k] = 1
k² + kn - 1 = 0
Resolvendo por Bhaskara :
k = [- n ± √(n² + 4)] / 2
Sabemos que k > 0, assim:
k = [- n + √(n² + 4)] / 2 (2)
Substituindo (2) em (1):
h = 2 log{[- n + √(n² + 4)] / 2 + n}
h = 2 log{[n + √(n² + 4)] / 2}
Resposta: Alternativa E.

Temos que:
log(k + n) = h/2
log k = -h/2
Assim:
2 log(k + n) = h (1)
-2 log k = h
Então
h = h
2 log(k + n) = -2log k
log(k + n) = - log k
log(k + n) + log k = 0
log[(k + n)k] = 0
elog[(k + n)k] = e0
[(k + n)k] = 1
k² + kn - 1 = 0
Resolvendo por Bhaskara :
k = [- n ± √(n² + 4)] / 2
Sabemos que k > 0, assim:
k = [- n + √(n² + 4)] / 2 (2)
Substituindo (2) em (1):
h = 2 log{[- n + √(n² + 4)] / 2 + n}
h = 2 log{[n + √(n² + 4)] / 2}
Resposta: Alternativa E.






