Questão 2e33ef18-88
Prova:ENEM 2011
Disciplina:Matemática
Assunto:Funções, Função de 1º Grau
Uma empresa de telefonia fixa oferece dois planos aos seus clientes: no plano K, o cliente paga R$ 29,90 por 200 minutos mensais e R$ 0,20 por cada minuto excedente; no plano Z, paga R$ 49,90 por 300 minutos mensais e R$ 0,10 por cada minuto excedente.
O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
Uma empresa de telefonia fixa oferece dois planos aos seus clientes: no plano K, o cliente paga R$ 29,90 por 200 minutos mensais e R$ 0,20 por cada minuto excedente; no plano Z, paga R$ 49,90 por 300 minutos mensais e R$ 0,10 por cada minuto excedente.
O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
O gráfico que representa o valor pago, em reais, nos dois planos em função dos minutos utilizados é
A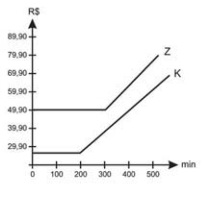

B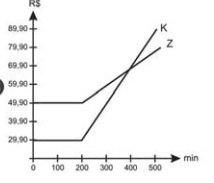

C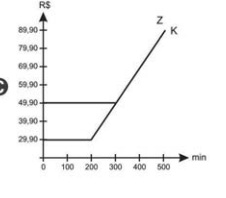

D
E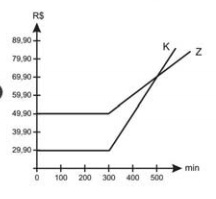

Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Montando as equações de acordo com o enunciado:
| 29,90 ; 0 ≤ x ≤ 200 (min)
k(x) = | ou
| 29,90 + 0,20(x - 200) ; x > 200 (min)
| 49,90 ; 0 ≤ x ≤ 300 (min)
z(x) = | ou
| 49,90 + 0,10(x - 300) ; x > 300 (min)
Obs: Os fatores (x - 200) e (x - 300), se devem ao fato de apenas estarmos considerando os minutos excedentes.
Encontrando agora o ponto onde estas retas se cruzam: k(x) = z(x)
29,90 + 0,20(x - 200) = 49,90 + 0,10(x - 300)
29,90 - 49,90 = 0,10x - 30 - 0,20x + 40
- 20 - 10 = - 0,10x
0,10x = 30
x = 300
Assim, a reta k(x) começa constante em 29.90 na ordenada até no ponto 200 na abcissa, daí começa a se inclinar linearmente. Já a reta z(x), começa constante em 49.9 na ordenada até o ponto 300 na abcissa, tendo justamente também neste ponto, um encontro com a reta k(x).
| 29,90 ; 0 ≤ x ≤ 200 (min)
k(x) = | ou
| 29,90 + 0,20(x - 200) ; x > 200 (min)
| 49,90 ; 0 ≤ x ≤ 300 (min)
z(x) = | ou
| 49,90 + 0,10(x - 300) ; x > 300 (min)
Obs: Os fatores (x - 200) e (x - 300), se devem ao fato de apenas estarmos considerando os minutos excedentes.
Encontrando agora o ponto onde estas retas se cruzam: k(x) = z(x)
29,90 + 0,20(x - 200) = 49,90 + 0,10(x - 300)
29,90 - 49,90 = 0,10x - 30 - 0,20x + 40
- 20 - 10 = - 0,10x
0,10x = 30
x = 300
Assim, a reta k(x) começa constante em 29.90 na ordenada até no ponto 200 na abcissa, daí começa a se inclinar linearmente. Já a reta z(x), começa constante em 49.9 na ordenada até o ponto 300 na abcissa, tendo justamente também neste ponto, um encontro com a reta k(x).
Assim, o único gráfico que descreve esse comportamento é o da letra D.
Resposta: Alternativa D.






