Um programador visual deseja modificar uma imagem,
aumentando seu comprimento e mantendo sua largura.
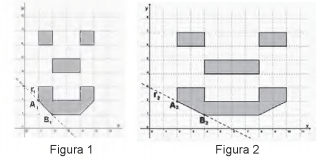
As figuras 1 e 2 representam, respectivamente, a imagem
original e a transformada pela duplicação do comprimento.
Para modelar todas as possibilidades de transformação
no comprimento dessa imagem, o programador precisa
descobrir os padrões de todas as retas que contêm os
segmentos que contornam os olhos, o nariz e a boca e,
em seguida, elaborar o programa.
No exemplo anterior, o segmento A1B1 da figura 1,
contido na reta r1, transformou-se no segmento A2B2 da
figura 2, contido na reta r2.
Suponha que, mantendo constante a largura da imagem,
seu comprimento seja multiplicado por n, sendo n um
número inteiro e positivo, e que, dessa forma, a reta r1
sofra as mesmas transformações. Nessas condições, o
segmento AnBn estará contido na reta rn .
A equação algébrica que descreve rn, no plano
cartesiano, é
Um programador visual deseja modificar uma imagem, aumentando seu comprimento e mantendo sua largura. As figuras 1 e 2 representam, respectivamente, a imagem original e a transformada pela duplicação do comprimento.

Para modelar todas as possibilidades de transformação no comprimento dessa imagem, o programador precisa descobrir os padrões de todas as retas que contêm os segmentos que contornam os olhos, o nariz e a boca e, em seguida, elaborar o programa.
No exemplo anterior, o segmento A1B1 da figura 1, contido na reta r1, transformou-se no segmento A2B2 da figura 2, contido na reta r2.
Suponha que, mantendo constante a largura da imagem, seu comprimento seja multiplicado por n, sendo n um número inteiro e positivo, e que, dessa forma, a reta r1 sofra as mesmas transformações. Nessas condições, o segmento AnBn estará contido na reta rn .
A equação algébrica que descreve rn, no plano
cartesiano, é






