
Admitindo que a linha pontilhada represente o gráfico da
função ƒ(x) = sen(x) e que a linha contínua represente o
gráfico da função g(x)= αsen(βx) segue que

Admitindo que a linha pontilhada represente o gráfico da função ƒ(x) = sen(x) e que a linha contínua represente o gráfico da função g(x)= αsen(βx) segue que









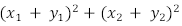 é igual a
é igual a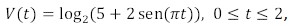

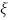 cuja parte imaginária é positiva. A parte real de
cuja parte imaginária é positiva. A parte real de 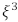 é igual a
é igual a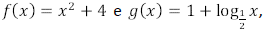 em que o domínio de
em que o domínio de 
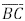 e
e 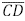 . Os segmentos
. Os segmentos 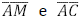 interceptam o segmento
interceptam o segmento 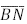 nos pontos
nos pontos 
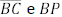 = 1. Os pontos R, S e T pertencem aos lados
= 1. Os pontos R, S e T pertencem aos lados 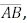
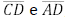 , respectivamente. O segmento
, respectivamente. O segmento 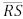 é paralelo a
é paralelo a 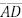 e intercepta
e intercepta 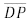 no ponto Q. O segmento
no ponto Q. O segmento 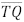 é paralelo a
é paralelo a 

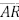 , o maior valor da soma das áreas do retângulo
, o maior valor da soma das áreas do retângulo 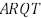 , do triângulo CQP e do triângulo DQS, para x variando no intervalo aberto ] 0,3[, é
, do triângulo CQP e do triângulo DQS, para x variando no intervalo aberto ] 0,3[, é

 , passa o plano α paralelo às arestas
, passa o plano α paralelo às arestas  e
e  . Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
. Dado que AP = 3, o quadrilátero determinado pelas interseções de α com as arestas do tetraedro tem área igual a
 e
e  são retos, AB = AD = 1, BC = CD = 2 e
são retos, AB = AD = 1, BC = CD = 2 e  é uma diagonal.O cosseno do ângulo
é uma diagonal.O cosseno do ângulo  vale
vale