c9d479b7-2d
PUC - RS 2011 - Matemática - Polinômios
Ao visitar a Faculdade de Matemática em Coimbra, Tales fez amizade com um estudante, que lhe propôs a seguinte questão:
Um polinômio tem tantas raízes imaginárias quantas são as consoantes da palavra Coimbra, e o número de raízes reais é no máximo igual ao número de vogais. Então, o grau deste polinômio é um número n tal que
Ao visitar a Faculdade de Matemática em Coimbra, Tales fez amizade com um estudante, que lhe propôs a seguinte questão:
Um polinômio tem tantas raízes imaginárias quantas são as consoantes da palavra Coimbra, e o número de raízes reais é no máximo igual ao número de vogais. Então, o grau deste polinômio é um número n tal que
Um polinômio tem tantas raízes imaginárias quantas são as consoantes da palavra Coimbra, e o número de raízes reais é no máximo igual ao número de vogais. Então, o grau deste polinômio é um número n tal que
A

B

C

D

E

 representam as funções oferta e demanda, respectivamente, de um determinado produto, onde x é o preço unitário. Quando a oferta e a demanda forem iguais, o valor do preço x será de
representam as funções oferta e demanda, respectivamente, de um determinado produto, onde x é o preço unitário. Quando a oferta e a demanda forem iguais, o valor do preço x será de
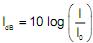 , onde I 0 = 10–12 W/m2 representa a intensidade sonora de referência de um som muito fraco percebido pelo ouvido humano.
, onde I 0 = 10–12 W/m2 representa a intensidade sonora de referência de um som muito fraco percebido pelo ouvido humano. 















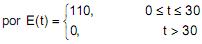
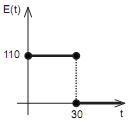
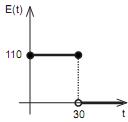
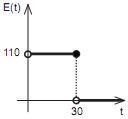
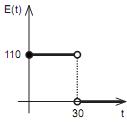
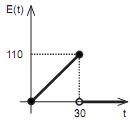
 de volta.
de volta. de volta.
de volta.