Um casal realiza sua mudança de domicílio
e necessita colocar numa caixa de papelão um
objeto cúbico, de 80 cm de aresta, que não pode ser
desmontado. Eles têm à disposição cinco caixas, com
diferentes dimensões, conforme descrito:
• Caixa 1: 86 cm x 86 cm x 86 cm
• Caixa 2: 75 cm x 82 cm x 90 cm
• Caixa 3: 85 cm x 82 cm x 90 cm
• Caixa 4: 82 cm x 95 cm x 82 cm
• Caixa 5: 80 cm x 95 cm x 85 cm
O casal precisa escolher uma caixa na qual o
objeto caiba, de modo que sobre o menor espaço livre
em seu interior.
A caixa escolhida pelo casal deve ser a de número
Um casal realiza sua mudança de domicílio e necessita colocar numa caixa de papelão um objeto cúbico, de 80 cm de aresta, que não pode ser desmontado. Eles têm à disposição cinco caixas, com diferentes dimensões, conforme descrito:
• Caixa 1: 86 cm x 86 cm x 86 cm
• Caixa 2: 75 cm x 82 cm x 90 cm
• Caixa 3: 85 cm x 82 cm x 90 cm
• Caixa 4: 82 cm x 95 cm x 82 cm
• Caixa 5: 80 cm x 95 cm x 85 cm
O casal precisa escolher uma caixa na qual o objeto caiba, de modo que sobre o menor espaço livre em seu interior.
A caixa escolhida pelo casal deve ser a de número










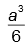
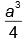
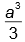
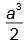
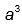
 . Se forem ordenados lado a lado, como é feito nas bibliotecas, eles ocuparão, linearmente, ________ cm.
. Se forem ordenados lado a lado, como é feito nas bibliotecas, eles ocuparão, linearmente, ________ cm. 


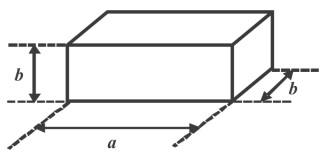
 é correto afirmar que a capacidade desse recipiente é, em mL, aproximadamente,
é correto afirmar que a capacidade desse recipiente é, em mL, aproximadamente,