Questõesde INSPER sobre Geometria Plana

InícioTodas as questões
1
1
1
Foram encontradas 37 questões
12ccd2c1-d8
INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Suponha que um dos triângulos que compõem o modelo de um arquivo STL tenha vértices cujas coordenadas, em relação a um sistema Oxyz ,sejam dadas por (a; 0; 0), (0; a; 0) e (a; a; a), sendo a>0. A área desse triângulo é igual a

O PASSO A PASSO DAS IMPRESSORAS 3D
A
a2√3 /2
B
a2√3 / 4
C
a2√2 / 4
D
a2 / 2
E
a2 / 4
12ba949f-d8
INSPER 2015 - Matemática - Polígonos, Geometria Plana

DA PERSPECTIVA DAS AVES: A FASCINANTE GEOMETRIA DA NOVA YORK VISTA DO CÉU
O fotógrafo americano Jeffrey Milstein é conhecido por suas imagens aéreas de cidades e bairros residenciais feitas a partir de helicóptero. Em seu mais recente projeto, Milstein foi para o céu acima de Nova York

"É longe o bastante para que a geometria da paisagem urbana, invisível quando vista do chão, apareça em padrões surpreendentes e, frequentemente, elegantes", acrescentou.

Disponível em: http://www1.folha.uol.com.br/bbc/2015/07/1655944‐da‐perspectiva‐das‐aves‐a‐fascinante‐geometria‐da‐nova‐york‐vista‐do‐ceu.shtml. Acesso em 11.10.15

Os tetos dos edifícios da foto aérea feita por Milstein revelam um padrão geométrico peculiar. A maioria dos edifícios mostrados apresenta dois pares de “saliências laterais”, mas também há alguns com três pares. Os tetos de todos eles podem ser associados a um polígono não convexo com certo número de lados. Por exemplo, para dois pares de “saliências laterais”, o polígono do teto tem 20 lados. Se generalizássemos esse padrão considerando um edifício com ݊ pares de “saliências laterais”, o polígono associado ao teto desse edifício teria um número de lados igual a

A
8n + 8
B
8n + 4
C
6n + 10
D
6n + 8
E
4n + 12
12523f12-d8
INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Admita que cada unidade de geração de energia da Ivanpah ocupa uma região circular de raio ܴ, cercada por espelhos que se estendem até os limites de uma região quadrada de lado L. Se a área da região ocupada pelos espelhos é 5 vezes a área da região onde fica localizada a unidade de geração de energia, então a relação entre L e R ܴ é dada por

Utilize a aproximação π = 3

Texto 1
A MAIOR USINA SOLAR DO MUNDO FICA NO DESERTO DA CALIFÓRNIA E É CAPAZ DE GERAR ENERGIA SUFICIENTE PARA 140 MIL CASAS
No meio do deserto da Califórnia, nos EUA, 300 mil espelhos trabalham sincronizados a um software especial para produzir energia. Trata‐se do Ivanpah Solar Electric Generating System, a maior usina termo solar do mundo, capaz de gerar energia suficiente para alimentar 140 mil casas. Assim como qualquer usina de energia, a Ivanpah produz energia elétrica ao criar um vapor de alta temperatura e girar uma turbina. A diferença é que, em vez de usar energia fóssil ou nuclear para isso, é utilizado o calor do sol, que, direcionado às torres por meio do sistema inteligente de espelhos, aquece a água, criando o vapor. Ao todo são três unidades de geração de energia, que ocupam uma área equivalente a 14,2 quilômetros quadrados. A Ivanpah é gerenciada pela BrightSource Limitless e pela gigante Google, que tem investido pesado em projetos sustentáveis.
Contudo, a Ivanpah não é incrível apenas pelo seu resultado e tecnologia. Os 300 mil espelhos localizados no deserto são também um prato cheio ao olhar, conforme revelam as imagens abaixo.


Disponível em: http://www.hypeness.com.br/2014/09/a‐maior‐usina‐solar‐do‐mundo‐e‐espetaculo‐tambem‐para‐os‐olhos/. Acesso em 27.09.15

Texto 2

Prato:
Locuções
p. cheio   
fato que dá motivo para zombaria ou crítica        
‹ não faça escândalo, que isso é um p. cheio para a vizinhança maledicente ›
p. comercial   
m.q. prato feito ('refeição')
p. feito   
1 refeição barata, a preço fixo, que já vem servida no prato e consiste ger. de um tipo de carne acompanhado de arroz, feijão, legumes etc., e pode incluir ou não sobremesa e uma bebida não alcoólica; prato comercial, pê‐efe, sortido
2 fig. situação favorável, fato ou conjunto de fatos que leva a determinado objetivo ou que vem a calhar para determinado fim     
‹ a vaga na empresa foi um p. feito para o jovem recém‐formado ›
p. fundo   
o que tem maior profundidade e é us. para sopa; prato covo
p. raso   
prato pouco profundo, us. para comida sólida
p. único   
um só tipo de comida, que constitui uma refeição 

Disponível em: http://houaiss.uol.com.br/busca?palavra=prato. Acesso em: 19.09.15
A
L = R√5
B
L = 2R√3
C
L = R√15
D
L = 3R√2
E
L = 2R√5
12112191-d8
INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Os apartamentos do Copan têm diferentes configurações, de modo que a quantidade de apartamentos por andar varia entre os 32 andares. Considerando a quantidade total de apartamentos no edifício informada no texto e a sua distribuição nos andares, é necessariamente verdadeiro que



EDIFÍCIO COPAN

O Copan foi projetado no início da década de 1950 na cidade de São Paulo, tendo como autor o arquiteto Oscar Niemeyer (...) num contexto de aquecimento do setor imobiliário na cidade, tornando‐se o maior edifício de habitação coletiva da América Latina (116.152m² de área total construída).
O projeto resulta na ocupação de terreno de área de 6.006,35 m², possuindo 1160 apartamentos distribuídos ao longo de 32 andares (...).


A
existem andares com 36 apartamentos.
B
nenhum andar pode ter menos do que 36 aparta‐ mentos.
C
pelo menos um andar deve ter mais do que 36 apartamentos.
D
existe um andar com 37 apartamentos.
E
nenhum andar pode ter mais do que 37 apartamentos.
120daba9-d8
INSPER 2015 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Porcentagem, Geometria Plana

Oscar Niemeyer projetou o Copan como um edifício curvo para aproveitar da melhor maneira possível um terreno que não era retangular. Considerando que a área total construída esteja igualmente distribuída em todos os andares da edificação, a porcentagem do terreno que o arquiteto conseguiu aproveitar com o seu projeto foi aproximadamente



EDIFÍCIO COPAN

O Copan foi projetado no início da década de 1950 na cidade de São Paulo, tendo como autor o arquiteto Oscar Niemeyer (...) num contexto de aquecimento do setor imobiliário na cidade, tornando‐se o maior edifício de habitação coletiva da América Latina (116.152m² de área total construída).
O projeto resulta na ocupação de terreno de área de 6.006,35 m², possuindo 1160 apartamentos distribuídos ao longo de 32 andares (...).


A
55%.
B
60%.
C
65%.
D
70%.
E
75%.
8f972140-d8
INSPER 2018 - Matemática - Áreas e Perímetros, Geometria Plana

A triangulação utilizando estações móveis ou fixas é uma técnica de rastreamento de aves que pode ser utilizada para
confirmar a presença de uma ave, que está sendo monitorada, em certo local.

A figura a seguir ilustra esse procedimento:


Considere um grupo de pesquisadores que está analisando a movimentação de pássaros no entorno de uma gruta. As retas r, s, e t, definidas para cada antena, estão descritas pelas seguintes equações:

ANTENA 1 => r: 4y + x – 29 = 0
ANTENA 2 => s: y – x – 1 = 0
ANTENA 3 => t: y + 4x – 11 = 0

Sabendo-se que, no sistema de coordenadas utilizados para definir essas equações, a distância linear unitária corresponde a 10 metros no espaço real, então a área de cobertura dessa telemetria é igual a

A
300 m² .
B
900 m² .
C
750 m² .
D
105 m² .
E
75 m² .
8f56897c-d8
INSPER 2018 - Matemática - Áreas e Perímetros, Geometria Plana

Após uma grande fabricante adotar o chamado entalhe (notch) para aumentar a área útil da tela dos celulares, essa técnica passou a estar presente em diversos modelos de diversas marcas. Comercialmente, o tamanho da tela de um celular é dado pela medida da sua diagonal em polegadas. Em um celular com entalhe, o procedimento é o mesmo, entretanto, a área real da tela será menor que a área de um celular sem entalhe, com a mesma diagonal.


Considere um celular, cuja tela retangular é de 5 polegadas e possui medidas laterais na proporção de 18:9. Esse aparelho possui um entalhe retangular ocupando 2/3 da largura da tela por 0,3 polegadas de altura, conforme ilustrado na figura acima.


Considerando , então a área real da tela do celular em questão, em polegadas ao quadrado, é um valor entre

A
9,6 e 9,7.
B
9,5 e 9,6.
C
9,3 e 9,4.
D
9,4 e 9,5.
E
9,7 e 9,8.
8d4bfc90-d8
INSPER 2018 - Matemática - Áreas e Perímetros, Geometria Plana

Considerando que esse crescimento se repita nos próximos séculos, a área A, em milhões de quilômetros quadrados, que o Saara ocupará daqui a n anos pode ser descrita, em função de n, pela lei

Leia a notícia para responder a questão

Considerado o maior deserto quente do mundo, o Saara encontra-se em expansão. Cresceu 10% no último século e hoje ocupa uma área de quase 7400000 de quilômetros quadrados (km² ), um pouco menor que a do Brasil.

(Pesquisa Fapesp. http://revistapesquisa.fapesp.br/ 2018/05/21/saara-cresce-10-em-um-seculo. Adaptado)
A
A(n) = 7,4·0,10,01·n .
B
A(n) = 7,4·1,10,01·n
C
A(n) = 7,4·1,1n.
D
A(n) = 7,4·0,1100·n .
E
A(n) = 7,4·1,1100·n .
8f3a4333-d8
INSPER 2018 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Áreas e Perímetros, Geometria Plana

Uma das áreas de testes utilizadas na pesquisa era circular, com raio igual a 100 metros. Dado que 1 hectare (ha) equivale a 10000 m2 e que a quantidade de P2 O5 aplicada foi proporcional a 50 kg por hectare, a produção de soja obtida na área em questão, segundo a fórmula apresentada, foi de, aproximadamente,

Leia o texto para responder a questão.

A deficiência de fósforo nos solos brasileiros se manifesta na baixa produtividade. Para reverter esse problema, uma equipe de agrônomos acompanhou a lavoura de um grupo de pequenos produtores, de modo a obter uma relação entre a produção S(n) de soja, em quilogramas por hectare (kg/ha), e a quantidade n de P2 O5 aplicada no solo, em kg/ha, e obteve a seguinte lei:

S(n) = 900 + 24·n – 0,05n2 , com 0 ≤ n ≤ 300
A
3100 kg.
B
31000 kg.
C
620 kg.
D
6200 kg.
E
62000 kg.
8d47a583-d8
INSPER 2018 - Matemática - Áreas e Perímetros, Geometria Plana

Baseando-se nos dados da notícia, é correto dizer que, um século atrás, o deserto do Saara ocupava uma área, em km² , de aproximadamente

Leia a notícia para responder a questão

Considerado o maior deserto quente do mundo, o Saara encontra-se em expansão. Cresceu 10% no último século e hoje ocupa uma área de quase 7400000 de quilômetros quadrados (km² ), um pouco menor que a do Brasil.

(Pesquisa Fapesp. http://revistapesquisa.fapesp.br/ 2018/05/21/saara-cresce-10-em-um-seculo. Adaptado)
A
6,67 · 106 .
B
6,67 · 107 .
C
6,73 · 106 .
D
6,67 · 105 .
E
6,73 · 107 .
18cd2f95-d8
INSPER 2015 - Matemática - Polígonos, Geometria Plana

O quadrilátero ABCD indicado na figura possui ângulo reto em A, um ângulo externo de 60° em B e três lados de medidas conhecidas que são AB = 7cm, BC = 6cm e C = 12cm.


Nesse quadrilátero, a medida de 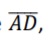 em centímetros, é igual a

A
3(2 + √3)
B
2(√11 + 3√3)
C
2(√11 + √3)
D
9√3
E
12√3
18c54c8a-d8
INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Para que não seja formada nenhuma sombra na projeção de luz feita pelo canhão, não pode haver nenhum objeto posicionado no espaço indicado pela região sombreada na figura, cuja área é igual a

A equipe que está preparando os efeitos de iluminação de um show a ser feito em um estádio precisa instalar um canhão de luz num ponto a 20 metros de altura em relação ao chão, no qual está posicionado um palco de 20 metros de comprimento onde o cantor irá se apresentar. Para definir o ângulo de movimentação do canhão de luz de modo que ele possa acompanhar o cantor por todo o palco, a equipe modelou o problema utilizando o plano cartesiano abaixo, no qual cada unidade equivale a 10 metros.

A
2 m2 .
B
4 m2 .
C
20 m2 .
D
40 m2 .
E
200 m2 .
189101a3-d8
INSPER 2015 - Matemática - Circunferências e Círculos, Geometria Plana

A linha curva indicada na figura tem extremidades em A e B e é formada apenas por semicircunferências.

Se o comprimento de AB é igual a x ,então o comprimento da linha curva será igual a

A

B

C

D

E

1895aff1-d8
INSPER 2015 - Matemática - Geometria Plana, Triângulos

Na figura, ABC é um triângulo equilátero, com A(0,0) e C(12,0) , e r é uma reta perpendicular ao eixo x em xo.

A função real f é tal que f(xo) é a área do polígono determinado pela intersecção do triângulo ABC com a região do plano definida pela relação x < xo. Em tais condições, a lei da função ݂fno intervalo real 0 < xo < 6 é

A
f(xo) = √3 xo2
B
f(xo) = 1/2 xo2
C
f(xo) = √2/2 xo2
D
f(xo) = √3/3 xo2
E
f(xo) = √3/2 xo2
1881a09e-d8
INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

A figura indica um bloco maciço com formato de paralelepípedo reto‐retângulo. As áreas das faces indicadas por A, B e C são, respectivamente, 48 cm², 32 cm² e 24 cm².

O número de blocos como esse que devem ser mergulhados em um tanque completamente cheio de água para que haja um transbordamento de exatamente 4,8 litros de líquido é igual a

A
28.
B
25.
C
24.
D
20.
E
18.
1879b263-d8
INSPER 2015 - Matemática - Áreas e Perímetros, Geometria Plana

As retas  interceptam-se no ponto T do lado  do retângulo ABCD e os segmentos são paralelos, conforme mostra a figura.


Sabendo que 3QT = 2TA e que a área do triângulo PQT é igual a 12cm2, é correto concluir que a área do retângulo ABCD, em cm2, é igual a

A
36.
B
42.
C
54.
D
72.
E
108.
1870fce8-d8
INSPER 2015 - Matemática - Circunferências e Círculos, Geometria Plana

A base da agência de espionagem C.O.N.T.R.O.L.E. localiza‐se em um terreno plano, na origem de um sistema de coordenadas cartesianas medidas em quilômetros. Nos pontos A(6;0), B(0;6), C(-6;0) e D(0;-6) foram instalados radares com o intuito de alertar os agentes da base sobre possíveis ataques terrestres. Cada radar patrulha uma região circular de R km de raio. Para que a proteção seja efetiva, a região patrulhada por um radar deve interceptar as regiões patrulhadas por outros dois radares em pelo menos um ponto, como indicado na figura ao lado.
Nessas condições, para que a proteção seja efetiva, R deve valer, no mínimo,

A
4√3
B
4√2
C
3√3
D
3√2
E
4
18671ded-d8
INSPER 2015 - Matemática - Circunferências e Círculos, Geometria Plana

Na figura, o hexágono regular ABCDEF tem lado medindo 2 cm e o arco de circunferência CE tem centro no vértice A.
A área da região sombreada, em cm2 , é igual a

A

2π + √3

B
π + 2√3
C
π + √3
D
2π + √3
E
3π + √3
1853b4e3-d8
INSPER 2015 - Matemática - Circunferências e Círculos, Geometria Plana

Na figura, em que está representada a circunferência trigonométrica, P é a extremidade de um arco trigonométrico da 1a . volta cuja medida, em radianos, é igual a α. Observe que P é um ponto do 2o quadrante localizado no interior do retângulo ABCD.


As coordenadas dos vértices do retângulo são dadas por:

Assim, é necessariamente verdadeira a desigualdade

A

B

C

D

E

0f847598-b1
INSPER 2016 - Matemática - Aritmética e Problemas, Álgebra, Áreas e Perímetros, Problemas, Geometria Plana, Frações e Números Decimais

O tempo necessário para que o número real de indivíduos seja o dobro do seu tamanho inicial excede o tempo estimado pelo potencial biótico para esse mesmo feito em

Adote: ln2 = 0,7 e ln3 = 1,1

Leia o texto a seguir para responder à questão.

    O potencial biótico de uma população corresponde à sua capacidade potencial para aumentar seu número de indivíduos em condições ideais. Na natureza, entretanto, verifica-se que o tamanho das populações em comunidades estáveis não aumenta indefinidamente, sendo que, à medida que a população cresce, aumenta a resistência ambiental, reduzindo o potencial biótico. Isso ocorre até que se estabeleça um equilíbrio, como apresentado no esquema a seguir.

Considere uma população que se estabeleceu em uma área, inicialmente com 10 indivíduos, cujo crescimento foi analisado ao longo dos últimos 50 anos. Sejam P(t) o número de indivíduos dessa população, segundo o potencial biótico, após t anos do início da análise, e N(t) o número real de indivíduos da população após t anos da análise, descritos pelas seguintes funções:


A
6 anos.
B
12 anos.
C
10 anos.
D
8 anos.
E
4 anos.