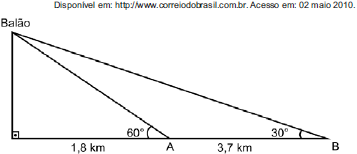
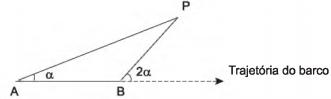
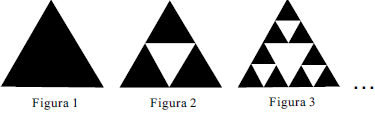
c025c4d1-bb
ENEM 2010 - Matemática - Áreas e Perímetros, Circunferências e Círculos, Geometria Plana
A ideia de usar rolos circulares para deslocar objetos pesados provavelmente surgiu com os antigos egípcios ao construírem as pirâmides.

Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é
A ideia de usar rolos circulares para deslocar objetos pesados provavelmente surgiu com os antigos egípcios ao construírem as pirâmides.

Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é

Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é
A
y = R.
B
y = 2R.
C
y =  R.
R.
 R.
R.D
y = 2 R.
R.
 R.
R.E
y = 4 R.
R.
 R.
R.