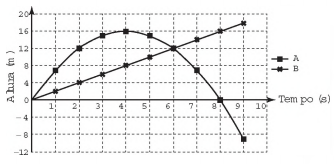
Considere que o modelo matemático utilizado no
estudo da velocidade V, de uma partícula de um fluido
escoando em um tubo, seja diretamente proporcional à
diferença dos quadrados do raio R da secção transversal
do tubo e da distância x da partícula ao centro da secção
que a contém. Isto é, V(x) = K2
(R2 - x2
), em que K é uma
constante positiva.
O valor de x, em função de R, para que a velocidade de
escoamento de uma partícula seja máxima é de
Considere que o modelo matemático utilizado no estudo da velocidade V, de uma partícula de um fluido escoando em um tubo, seja diretamente proporcional à diferença dos quadrados do raio R da secção transversal do tubo e da distância x da partícula ao centro da secção que a contém. Isto é, V(x) = K2 (R2 - x2 ), em que K é uma constante positiva.
O valor de x, em função de R, para que a velocidade de escoamento de uma partícula seja máxima é de







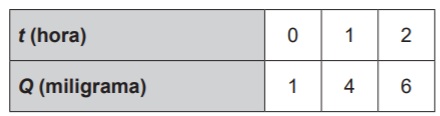















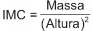 , na qual a massa é em quilograma e a altura, em metro. As crianças,
naturalmente, começam a vida com um alto índice
de gordura corpórea, mas vão ficando mais magras
conforme envelhecem, por isso os cientistas criaram um
IMC especialmente para as crianças e jovens adultos, dos
dois aos vinte anos de idade, chamado de IMC por idade.
, na qual a massa é em quilograma e a altura, em metro. As crianças,
naturalmente, começam a vida com um alto índice
de gordura corpórea, mas vão ficando mais magras
conforme envelhecem, por isso os cientistas criaram um
IMC especialmente para as crianças e jovens adultos, dos
dois aos vinte anos de idade, chamado de IMC por idade.