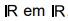Questões UNESP sobre Funções | Pratique com o Prisma

UNESP 2021 - Matemática - Funções, Função de 2º Grau

O dono de uma empresa dispunha de recurso para equipá-la com novos maquinários e empregados, de modo a aumentar a produção horária de até 30 itens. Antes de realizar o investimento, optou por contratar uma equipe de consultoria para analisar os efeitos da variação v da produção horária dos itens no custo C do produto. Perante as condições estabelecidas, o estudo realizado por essa equipe obteve a seguinte função:

A equipe de consultoria sugeriu, então, uma redução na produção horária de 10 itens, o que permitiria enxugar o quadro de funcionários, reduzindo o custo, sem a necessidade de investir novos recursos.

O dono da empresa optou por não seguir a decisão e questionou qual seria o aumento necessário na produção horária para que o custo do produto ficasse igual ao obtido com a redução da produção horária proposta pela consultoria, mediante os recursos disponibilizados.

De acordo com a função obtida, a equipe de consultoria deve informar que, nesse caso,

A

é impossível igualar o custo da redução proposta, pois os recursos disponíveis são insuficientes, uma vez que essa igualdade exigiria um aumento na produção horária de 50 itens.

B

é possível igualar o custo da redução proposta, uma vez que essa igualdade exigiria um aumento na produção horária de 15 itens, o que está dentro dos recursos disponíveis.

C

é possível igualar o custo da redução proposta, uma vez que essa igualdade exigiria um aumento na produção horária de 20 itens, o que está dentro dos recursos disponíveis.

D

é impossível igualar o custo da redução proposta, pois os recursos disponíveis são insuficientes, uma vez que essa igualdade exigiria um aumento na produção horária de 40 itens.

E

é possível igualar o custo da redução proposta, desde que sejam empregados todos os recursos disponíveis, uma vez que essa igualdade exigiria um aumento na produção horária de 30 itens.

ffd24dae-6a

UNESP 2021 - Matemática - Funções, Logaritmos, Equação Logarítmica

Desenvolvida em 1935 por Charles F. Richter, com a colaboração de Beno Gutenberg, a escala Richter permite determinar a magnitude (M) de um terremoto, fenômeno que libera uma grande quantidade de energia (E) que se propaga pela Terra em todas as direções. A magnitude e a energia de um terremoto podem ser relacionadas pela expressão a seguir, em que E é expressa em erg, uma unidade de medida de energia do sistema CGS.

logE = 11,8 + 1,5M

A tabela apresenta os efeitos gerados por um terremoto, de acordo com sua magnitude na escala Richter:

No dia 6 de janeiro de 2020, o sul de Porto Rico foi atingido por um terremoto que liberou uma quantidade de energia E = 10^13,8 J. Considerando a tabela e que 1 erg = 10–7 J, esse terremoto

A

foi destrutivo em áreas até 100 km do epicentro.

B

danificou casas mal construídas em regiões próximas ao epicentro.

C

não foi sentido e não causou danos.

D

causou sérios danos em uma grande faixa, sendo considerado um grande terremoto.

E

causou graves danos em áreas a centenas de quilômetros do epicentro, sendo considerado um enorme terremoto.

002bba1a-0a

UNESP 2018 - Matemática - Funções, Função de 2º Grau

Em relação a um sistema cartesiano de eixos ortogonais com origem em O(0, 0), um avião se desloca, em linha reta, de O até o ponto P, mantendo sempre um ângulo de inclinação de 45º com a horizontal. A partir de P, o avião inicia trajetória parabólica, dada pela função f(x) = –x2 + 14x – 40, com x e f(x) em quilômetros. Ao atingir o ponto mais alto da trajetória parabólica, no ponto V, o avião passa a se deslocar com altitude constante em relação ao solo, representado na figura pelo eixo x.

Em relação ao solo, do ponto P para o ponto V, a altitude do avião aumentou

A

2,5 km.

B

3 km.

C

3,5 km.

D

4 km.

E

4,5 km.

3336da17-58

UNESP 2018 - Matemática - Análise de Tabelas e Gráficos, Funções, Equações Exponenciais

Observe, no plano cartesiano de eixos ortogonais, o gráfico de duas funções exponenciais de

A intersecção desses gráficos ocorrerá em

A

infinitos pontos, localizados no 2° quadrante.

B

um único ponto, localizado no 2° quadrante.

C

um único ponto, localizado no 3° quadrante.

D

um único ponto, localizado no 1° quadrante.

E

um único ponto, localizado no 4° quadrante.

332bac6d-58

UNESP 2018 - Matemática - Quadriláteros, Funções, Geometria Plana, Polinômios, Função de 2º Grau

Sendo x um número real maior que 2/3 , a área de um retângulo é dada pelo polinômio 3x2 + 19x –14. Se a base desse retângulo é dada pelo polinômio x + 7, o quadrado da diagonal do retângulo é expresso pelo polinômio

A

10x2 + 26x + 29.

B

10x2 + 53.

C

10x2 + 65.

D

4x2 + 2x + 53.

E

10x2 + 2x + 53.

3429d23e-1b

UNESP 2017 - Matemática - Funções, Função de 2º Grau

Os pontos P e Q(3, 3) pertencem a uma circunferência centrada na origem do plano cartesiano. P também é ponto de intersecção da circunferência com o eixo y.

Considere o ponto R, do gráfico de y = √x , que possui ordenada y igual à do ponto P. A abscissa x de R é igual a

A

9.

B

16.

C

15.

D

12.

E

18.

c6badd53-3b

UNESP 2017 - Matemática - Funções, Função de 1º Grau, Álgebra Linear, Sistemas Lineares

Um grupo de estudantes fará uma excursão e alugará ônibus para transportá-lo. A transportadora dispõe de ônibus em dois tamanhos, pequeno e grande. O pequeno tem capacidade para 24 pessoas, ao custo total de R$ 500,00. O grande tem capacidade para 40 pessoas, ao custo total de R$ 800,00. Sabe-se que pelo menos 120 estudantes participarão da excursão e que o grupo não quer gastar mais do que R$ 4.000,00 com o aluguel dos ônibus.
Sendo x o número de ônibus pequenos e y o número de ônibus grandes que serão alugados, o par ordenado (x, y) terá que pertencer, necessariamente, ao conjunto solução do sistema de inequações

A

B

C

D

E

cfb26dbc-29

UNESP 2016 - Matemática - Funções, Equações Exponenciais

A figura descreve o gráfico de uma função exponencial do tipo y = ax , de |R em |R.

Nessa função, o valor de y para x = –0,5 é igual a

A

log5

B

log₅2

C

√5

D

log₂5

E

2,5

cfa2ed7a-29

UNESP 2016 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

Em um experimento com sete palitos de fósforo idênticos, seis foram acesos nas mesmas condições e ao mesmo tempo. A chama de cada palito foi apagada depois de t segundos e, em seguida, anotou-se o comprimento x, em centímetros, de madeira não chamuscada em cada palito. A figura a seguir indica os resultados do experimento.

Um modelo matemático consistente com todos os dados obtidos no experimento permite prever que o tempo, necessário e suficiente, para chamuscar totalmente um palito de fósforo idêntico aos que foram usados no experimento é de

A

1 minuto e 2 segundos.

B

1 minuto.

C

1 minuto e 3 segundos.

D

1 minuto e 1 segundo.

E

1 minuto e 4 segundos.

e969491e-94

UNESP 2011 - Matemática - Funções, Equações Exponenciais

Baseado nesse modelo, e tomando a aproximação para o logarítmo natural ln (14/95) ≅ -1,9 a população brasileira será 90% da suposta população de estabilização aproximadamente no ano de:

Em 2010, o Instituto Brasileiro de Geografia e Estatística (IBGE) realizou o último censo populacional brasileiro, que mostrou que o país possuía cerca de 190 milhões de habitantes. Supondo que a taxa de crescimento populacional do nosso país não se altere para o próximo século, e que a população se estabilizará em torno de 280 milhões de habitantes, um modelomatemático capaz de aproximar o número de habitantes (P),em milhões, a cada ano (t), a partir de 1970, é dado por:

P(t) = [280 – 190 · e^{– 0,019} · ^{(t – 1970)}].

A

2065.

B

2070.

C

2075.

D

2080.

E

2085.

3db4f14c-8d

UNESP 2011 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

A tabela apresenta, na coluna da esquerda, a descrição de alguns tipos de funções e, na coluna da direita, representações de alguns gráficos de funções, cujas variáveis independentes, definidas no domínio dos números reais, estão representadas nos eixos das abscissas.

O conjunto de pares ordenados que relaciona cada função à sua respectiva representação gráfica é:

A

{(I, a), (II, d), (III, e), (IV, b), (V, c)}.

B

{(I, c), (II, d), (III, a), (IV, b), (V, e)}.

C

{(I, d), (II, e), (III, a), (IV, b), (V, c)}.

D

{(I, e), (II, d), (III, a), (IV, b), (V, c)}.

E

{(I, e), (II, d), (III, b), (IV, a), (V, c)}.

061b06c9-8d

UNESP 2010 - Matemática - Aritmética e Problemas, Porcentagem, Funções, Equações Exponenciais

Ambientalistas, após estudos sobre o impacto que possa vir a ser causado à população de certa espécie de pássaros pela construção de um grande conjunto de edifícios residenciais próximo ao sopé da Serra do Japi, em Jundiaí, SP, concluíram que a quantidade de tais pássaros, naquela região, em função do tempo, pode ser expressa, aproximadamente, pela função

onde t representa o tempo, em anos, e P0 a população de pássaros na data de início da construção do conjunto. Baseado nessas informações, pode-se afirmar que:

A

após 1 ano do início da construção do conjunto, P(t) estará reduzida a 30% de P0.

B

após 1 ano do início da construção do conjunto, P(t) será reduzida de 30% de P0.

C

após 2 anos do início da construção do conjunto, P(t) estará reduzida a 40% de P0.

D

após 2 anos do início da construção do conjunto, P(t) será reduzida de 40% de P0.

E

P(t) não será inferior a 25% de P0.

115613eb-36

UNESP 2010 - Matemática - Funções, Função de 1º Grau, Polinômios, Função de 2º Grau

Através dos gráficos das funções f(x) e g(x), os valores de f(g(0)) e g(f(1)) são, respectivamente:

A

–5 e 0.

B

–5 e 2.

C

0 e 0.

D

2 e –5.

E

2 e 0.

11421149-36

UNESP 2010 - Matemática - Funções, Função de 1º Grau

Observe o gráfico da função f(x) e analise as afirmações a seu respeito.

I. Se x1 , x2 ∈ Dom(f) e x2 > x1 , então f(x2 ) > f(x1 ).

II. Se x > 1, então f(x) < 0.

III. O ponto (2, –2) pertence ao gráfico de f(x).

IV. A lei de formação de f(x) representada no gráfico é dada por f(x) = - 1/2 ( x -1).

A alternativa que corresponde a todas as afirmações verdadeiras é:

A

I e III.

B

I, II e III.

C

I e IV.

D

II, III e IV.

E

II e IV.

f1a1ddc0-d6

UNESP 2014 - Matemática - Funções, Equações Exponenciais

No artigo “Desmatamento na Amazônia Brasileira: com que intensidade vem ocorrendo?”, o pesquisador Philip M. Fearnside, do INPA, sugere como modelo matemático para o cálculo da área de desmatamento a função D(t) = D(0) · e^k·t , em que D(t) representa a área de desma- tamento no instante t, sendo t medido em anos desde o instante inicial, D(0) a área de desmatamento no instante inicial t = 0, e k a taxa média anual de desmatamento da região. Admitindo que tal modelo seja representativo da realidade, que a taxa média anual de desmatamento (k) da Amazônia seja 0,6% e usando a aproximação In2 ≅ 0,69 , o número de anos necessários para que a área de desmatamento da Amazônia dobre seu valor, a partir de um instante inicial prefixado, é aproximadamente

A

51.

B

115.

C

15.

D

151.

E

11.

c7a834d3-9f

UNESP 2013 - Matemática - Aritmética e Problemas, Porcentagem, Funções, Logaritmos

Caso a velocidade média do trânsito nos principais corredores viários paulistanos continue decaindo nos mesmos percentuais pelos próximos anos e sabendo que ln 2 ≈ 0,69, ln 3 ≈ 1,10, ln 5 ≈ 1,61 e ln 19 ≈ 2,94, os anos aproximados em que as velocidades médias nos picos da manhã e da tarde chegarão à metade daquelas observadas em 2012 serão, respectivamente

O que era impressão virou estatística: a cidade de São Paulo está cada dia mais lenta. Quem mostra é a própria CET (Companhia de Engenharia de Tráfego), que concluiu um estudo anual sobre o trânsito paulistano.Os dados de 2012 apontam que a velocidade média nos principais corredores viários da cidade foi de 22,1 km/h no pico da manhã e de 18,5 km/h no pico da tarde. Uma piora de 5% e 10% em relação a 2008, respectivamente.

A

2028 e 2019

B

2068 e 2040

C

2022 e 2017

D

2025 e 2018.

E

2057 e 2029.

3b0a9234-78

UNESP 2012 - Matemática - Funções, Logaritmos

Todo número inteiro positivo n pode ser escrito em sua notação científica como sendo n = k ·10^x, em que k ∈ **R*,** 1 ≤ k < 10 e x ∈ Z. Além disso, o número de algarismos de n é dado por (x + 1).

Sabendo que log 2 &cong; 0,30, o número de algarismos de 2⁵⁷ é

A

16.

B

19.

C

18.

D

15.

E

17.

Questõesde UNESP sobre Funções

Observe, no plano cartesiano de eixos ortogonais, o gráfico de duas funções exponenciais de A intersecção desses gráficos ocorrerá em