Questõessobre Triângulos

InícioTodas as questões
1
1
Foram encontradas 376 questões
2710e114-7a
ENEM 2022 - Matemática - Polígonos, Geometria Plana, Triângulos

Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18, 14 e 12 cm.


Posteriormente, a peça triangular ABC foi dobrada, de tal maneira que o vértice B ficou sobre o segmento , e o segmento  ficou paralelo ao lado , conforme Figura 2.






Sabe-se que, na Figura 1, o ângulo AĈB é menor que o ângulo CÂB e este é menor que o ângulo , e que os cortes e dobraduras foram executados corretamente pelas máquinas.


Nessas condições, qual é o valor da soma dos comprimentos, em centímetro, dos segmentos  e  ?

A
19
B
20
C
21
D
23
E
24
d8728bbc-73
USP 2021 - Matemática - Geometria Plana, Triângulos

Um deltaedro é um poliedro cujas faces são todas triângulos equiláteros. Se um deltaedro convexo possui 8 vértices, então o número de faces desse deltaedro é: 


Note e adote:
Em poliedros convexos, vale a relação de Euler F = A + V = 2, em que F é o número de faces, A é o número de arestas e V é o número de vértices do poliedro.

A
4
B
6
C
8
D
10
E
12
ffc77689-58
UECE 2021 - Matemática - Geometria Plana, Triângulos

Desejando-se cercar uma área plana na forma de um triângulo cujos vértices estão nos pontos X, Y e Z, ao iniciar a construção da cerca, verificou–se que a localização do ponto Y tinha desaparecido. O mapa indicava que o comprimento do lado XZ era 20 m e o comprimento do lado YZ era 30 m. Além disso, o ângulo (interno ao triângulo) entre ZX e XY era 120 graus. Nestas condições, pode-se afirmar corretamente que o comprimento do lado XY, em metros, é aproximadamente


Se precisar, use o número 49 como valor aproximado de √2400.

A
13,6.
B
14,5.
C
14,0.
D
15,1.
608c42e0-09
UEA 2018 - Matemática - Áreas e Perímetros, Polígonos, Geometria Plana, Triângulos

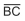
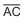
De uma chapa metálica, com a forma do triângulo retângulo ABC, retirou-se uma região retangular AMNP, conforme indicado na figura. Sabe-se que BC.1.png (25×21) mede 56 cm, que M é ponto médio de AC.png (25×25) e que a medida de é 30º.



Usando √3=1,73, AP + AM mede, aproximadamente,

A
32,8 cm.
B
38,2 cm.
C
40,2 cm.
D
36,1 cm.
E
35,1 cm.
32b7ae47-0b
UECE 2021 - Matemática - Geometria Plana, Triângulos

No triângulo XYZ, a mediatriz do lado YZ contém a mediana relativa ao vértice X, a medida desta mediana é igual a 2 cm e a medida do lado XY é igual a 3 cm. Se P é o ponto da reta que contém o lado XY tal que ZP é perpendicular a esta reta, então, a medida, em cm2 , da área do triângulo PYZ é igual a

A

B

C

D

0fd5e475-04
FGV 2020 - Matemática - Geometria Plana, Triângulos

As coordenadas cartesianas dos vértices da base do triângulo isósceles FGV são F(6, 0) e G(0, 6). Sendo m e n os dois valores possíveis de abscissa de V para que a área de FGV seja igual a 6 unidades de área do plano cartesiano, o valor de m + n é

A
5
B
11/2
C
6
D
13/2
E
7
0fe8101e-04
FGV 2020 - Matemática - Geometria Plana, Triângulos

A figura indica o triângulo FGV, com ângulo reto em V e medida do ângulo , em graus, igual a 2α. A bissetriz do ângulo intersecta em E.


Sabendo-se que GE = 6 cm e FE = 3 cm, a medida de , em cm, é igual a

A
3√5 - 4 cos α
B
√9 - 6 cos α
C
√9 - 6 cos (90° + α)
D
3√5 + 4 cos (90° + α)
E
3√5 - 4 cos (90° + α)
cc927339-03
UEA 2018 - Matemática - Áreas e Perímetros, Circunferências e Círculos, Geometria Plana, Triângulos

A figura mostra uma circunferência λ, de centro O, e um triângulo AOB, que tangencia a circunferência no ponto A.



Se senα = 1/2 e OA + OB = 9 cm, o comprimento da circunferência λ é igual a

A
12π cm.
B
6π cm.
C
8π cm.
D
3π cm.
E
9π cm.
a87c3d2e-02
UEG 2017 - Matemática - Polígonos, Geometria Plana, Triângulos

Na figura a seguir, a reta que passa pelos pontos A e B possui equação y = 2x - 1, ao passo que a reta que contém o ponto B e C é y = -2x + 11.



Dessa forma, a altura h na figura é

A
4,5
B
5,5
C
6,0
D
5,0
E
6,5
942eb67a-05
UFRGS 2016 - Matemática - Circunferências e Círculos, Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos

Um desenhista foi interrompido durante a realização de um trabalho, e seu desenho ficou como na figura abaixo.


Se o desenho estivesse completo, ele seria um polígono regular composto por triângulos equiláteros não sobrepostos, com dois de seus vértices sobre um círculo, e formando um ângulo de 40º, como indicado na figura.

Quando a figura estiver completa, o número de triângulos equiláteros com dois de seus vértices sobre o círculo é

A
10.
B
12.
C
14.
D
16.
E
18.
af680dab-ff
URCA 2016 - Matemática - Geometria Plana, Triângulos

O triângulo abaixo é isósceles, possui base igual a 30 e altura igual a 8. A área da região em destaque vale?


A
15/4 π
B
120 π
C
15/16 (120 − 4 π)
D
15/16 (128 − 15 π)
E
225/16 π
af5c266b-ff
URCA 2016 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Sendo M1=(6,4), M2=(7,1) e M3=(2,0) as coordenadas dos pontos médios dos vértices de um triângulo, podemos afirmar que a área deste triângulo vale:

A
76u . a.
B
64u . a.
C
52u . a .
D
46u . a.
E
32u . a.
ceef728d-fa
UFRGS 2019 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Considere o hexágono regular ABCDEF de lado 1. Sobre o lado do hexágono, constrói-se o quadrado AGHF, como mostra a figura abaixo. Sendo M o ponto médio de , constrói-se o triângulo CDM.



A área do triângulo CDM é

A
√3 - 1.
B

C

D
√3/4.
E
√3/2.
cefe03de-fa
UFRGS 2019 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Considere os pontos A, B e C, de coordenadas inteiras, que determinam os vértices do triângulo ABC, representado no sistema de coordenadas cartesianas abaixo.

A revolução do triângulo ABC, em torno do eixo x, gera o sólido P, e a revolução do triângulo ABC, em torno do eixo y, gera o sólido Q.



A razão entre os volumes de P e Q é  

A
2/3.
B
1.
C
3/2.
D
18.
E
36.
cee7374f-fa
UFRGS 2019 - Matemática - Polígonos, Geometria Plana, Triângulos

Na figura abaixo, tem-se um retângulo ABCD, de lados , e um triângulo equilátero BEC, construído sobre o lado



A medida de é

A


B


C
7.
D
√19.
E


8cc5d042-f8
UEG 2015 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Na figura a seguir tem-se que .



A área do triângulo DGH destacado pode ser dada pela expressão:

A

B

C

D

bb71a1c7-f7
UEG 2016 - Matemática - Pontos e Retas, Geometria Analítica, Geometria Plana, Triângulos

Na figura a seguir, os pontos A, B, C formam um triângulo equilátero de lado x, os pontos A, C, D, E um quadrado e o segmento BF é o dobro do tamanho de CD.




Considerando-se os dados apresentados, verifica-se que a distância do ponto F ao ponto E é

A

B


C
x2 + √3x
D

E
x2(8 + √3)
504bb0cf-f7
UNEMAT 2016 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos

A cidade de Brasília (DF) foi projetada e seu mapa foi todo desenhado para ter o formato de um avião. Já Triangolândia foi projetada no formato de um triângulo, conforme a figura abaixo.


Qual é a medida da distância x?

A
6 km
B
5,5 km
C
5 km
D
7 km
E
8 km
7bf4e390-f6
UNINOVE 2015 - Matemática - Geometria Plana, Triângulos

Sejam M e N os pontos médios dos lados AC e AB, respectivamente, de um triângulo ABC de área S. Unindo-se os pontos M e N, forma-se o triângulo AMN, semelhante à ABC e com área valendo K% de S. É correto afirmar que K vale

A
25.
B
50.
C
40.
D
30.
E
35.
aef0b9bb-00
UDESC 2019 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Na Figura 2, o triângulo BDE é retângulo em E, a medida da hipotenusa é igual a 12/5 cm e a do cateto BE = 2 cm.



Considerando e BC = 12 cm, a área do triângulo ABC é igual a:

A
10√11 cm²
B
2√11 cm²
C
20√11 cm²
D
4√11 cm²
E
5√11 cm²