Questão 8e3904db-09
Prova:UFT 2012
Disciplina:Matemática
Assunto:Cone, Geometria Plana, Geometria Espacial
Em uma aula de matemática, o professor fez uma demonstração prática de como o nível da água de um recipiente sobe ao introduzir um objeto em seu interior. O professor utilizou um recipiente que tinha o formato do tronco de um cone reto e imergiu totalmente um cubo maciço neste recipiente. Esta demonstração está representada nas figuras a seguir
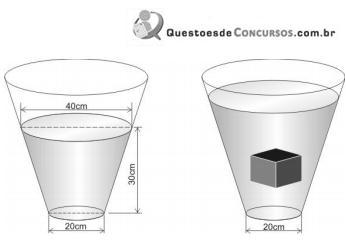
Durante a demonstração verificou-se que o volume do objeto é 
do volume de água já existente no recipiente.
Tomando por base a demonstração prática realizada pelo professor de matemática, conclui-se que a aresta do objeto introduzido no recipiente é (considere 
=3 )
Em uma aula de matemática, o professor fez uma demonstração prática de como o nível da água de um recipiente sobe ao introduzir um objeto em seu interior. O professor utilizou um recipiente que tinha o formato do tronco de um cone reto e imergiu totalmente um cubo maciço neste recipiente. Esta demonstração está representada nas figuras a seguir
Durante a demonstração verificou-se que o volume do objeto é do volume de água já existente no recipiente.
Tomando por base a demonstração prática realizada pelo professor de matemática, conclui-se que a aresta do objeto introduzido no recipiente é (considere=3 )
Durante a demonstração verificou-se que o volume do objeto é
do volume de água já existente no recipiente. Tomando por base a demonstração prática realizada pelo professor de matemática, conclui-se que a aresta do objeto introduzido no recipiente é (considere
=3 )A
3 cm
B
9 cm
C
D
E
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
O volume do tronco do cone é V1 = Πh/3[R2 + Rr + r2] Onde R = 40 cm, r = 20 cm, h = 30 cm e Π = 3. Substituindo:
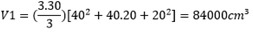
De acordo com o enunciado, o volume do objeto V2 = 3/7 de V1, assim:
V2 = (3/7).84000 = 36000 cm3, como V2 = a3 então a3 = 36000, logo a = 10∛9 cm
Letra D
