Questõesde UDESC 2017
A introdução de uma espécie X de peixe em um lago, onde normalmente inexiste esta espécie,
poderá provocar alteração do equilíbrio das populações de peixes autóctones.
Sobre esse fato, analise as proposições.
I. A espécie X morrerá, pois espécies introduzidas não sobrevivem em ambientes que não
sejam os seus.
II. O equilíbrio poderá ser alterado, se a espécie X for predadora dos peixes nativos.
III. O equilíbrio não será alterado, se a espécie X apresentar altas taxas reprodutivas e
cuidado parental.
IV. O equilíbrio poderá ser alterado, se houver competição por alimentos entre a espécie X e
as espécies nativas.
Assinale a alternativa correta.
Complete as lacunas.
________ são hormônios vegetais relacionados à regulação do crescimento das plantas.
Quando estimulados iniciam a síntese de enzimas que promovem o amolecimento da parede
celular, proporcionando movimentos vegetais como __________. Artificialmente, é
possível produzir _________ por meio da aplicação de ácido indolilacético diretamente nos
ovários para se obter uvas, melancias e tomates, sem sementes.
Assinale a alternativa que completa as lacunas do texto, corretamente.
No incêndio que atingiu o norte de Portugal, 42 pessoas morreram e centenas ficaram feridas,
embora os corpos das vítimas fatais ficassem queimados e irreconhecíveis, foi possível
preparar, a partir de fragmentos de tecidos, amostras de DNA nuclear e DNA mitocondrial de
todas vítimas. Entre as vítimas que faleceram no incêndio, estavam dois filhos do sexo
masculino de mães diferentes de um mesmo pai que não morreu no incêndio. Usando a
análise de DNA para a determinação da paternidade dos filhos, assinale a afirmação correta:
Um tubarão e um golfinho possuem muitas semelhanças morfológicas, embora pertençam a
grupos distintos. O tubarão é um peixe que respira por brânquias, e suas nadadeiras são
suportadas por cartilagens. O golfinho é um mamífero, respira ar atmosférico por pulmões, e
suas nadadeiras escondem ossos semelhantes aos dos nossos membros superiores. Portanto,
a semelhança morfológica existente entre os dois não revela parentesco evolutivo. Eles
adquiriram essa grande semelhança externa pela ação do ambiente aquático que selecionou
nas duas espécies a forma corporal ideal ajustada à água.
Esse processo é conhecido como:
Todos os seres vivos relacionam-se uns com outros, tanto entre indivíduos da mesma
espécie (relações intraespecíficas), quanto de espécies distintas (relações interespecíficas).
Essas relações podem ser harmônicas, quando não há prejuízo para nenhum dos indivíduos
envolvidos; ou desarmônicas, quando pelo menos um deles é prejudicado.
São relações desarmônicas:
Todos os seres vivos relacionam-se uns com outros, tanto entre indivíduos da mesma espécie (relações intraespecíficas), quanto de espécies distintas (relações interespecíficas). Essas relações podem ser harmônicas, quando não há prejuízo para nenhum dos indivíduos envolvidos; ou desarmônicas, quando pelo menos um deles é prejudicado.
São relações desarmônicas:
Resultados recentes de trabalhos de pesquisadores da Fiocruz, de Pernambuco, mostraram
que além do mosquito Aedes aegypti, o mosquito Culex quinquefasciatus, conhecido como
pernilongo ou muriçoca, também é capaz de transmitir o zika vírus.
Analise as proposições em relação à informação, e assinale (V) para verdadeira e (F) para
falsa.
( ) Novas medidas de controle populacional dos mosquitos serão necessárias, já que os
pernilongos Aedes e Culex possuem características genéticas diferentes.
( ) Esses resultados não trazem informações relevantes uma vez que todos os
mecanismos de transmissão do zika vírus já são conhecidos, assim como o tratamento
para a doença.
( ) Os vírus são seres vivos e agentes infecciosos diminutos, e como possuem
metabolismo próprio podem se replicar rapidamente no ambiente, por isso não é
aconselhavel deixar água parada em recipientes ao ar livre.
( ) O zika é um vírus transmitido pelo Aedes aegypti e pode-se dizer que é o mesmo vírus
da dengue, transmitida pelo mesmo mosquito, apenas mudando o nome da doença.
( ) Devido ao fato de ser uma doença causada por vírus, a confirmação da doença zika
vírus ocorre apenas por sintomas, não tendo outra forma de confirmação, a exemplo,
pelo exame de sangue.
Assinale a alternativa correta,de cima para baixo.
Resultados recentes de trabalhos de pesquisadores da Fiocruz, de Pernambuco, mostraram que além do mosquito Aedes aegypti, o mosquito Culex quinquefasciatus, conhecido como pernilongo ou muriçoca, também é capaz de transmitir o zika vírus.
Analise as proposições em relação à informação, e assinale (V) para verdadeira e (F) para falsa.
( ) Novas medidas de controle populacional dos mosquitos serão necessárias, já que os pernilongos Aedes e Culex possuem características genéticas diferentes.
( ) Esses resultados não trazem informações relevantes uma vez que todos os mecanismos de transmissão do zika vírus já são conhecidos, assim como o tratamento para a doença.
( ) Os vírus são seres vivos e agentes infecciosos diminutos, e como possuem metabolismo próprio podem se replicar rapidamente no ambiente, por isso não é aconselhavel deixar água parada em recipientes ao ar livre.
( ) O zika é um vírus transmitido pelo Aedes aegypti e pode-se dizer que é o mesmo vírus da dengue, transmitida pelo mesmo mosquito, apenas mudando o nome da doença.
( ) Devido ao fato de ser uma doença causada por vírus, a confirmação da doença zika vírus ocorre apenas por sintomas, não tendo outra forma de confirmação, a exemplo, pelo exame de sangue.
Assinale a alternativa correta,de cima para baixo.
“Escherichia coli é comum na flora bacteriana do intestino de humanos e de outros animais,
mas que em grandes quantidades pode causar problemas como infecção intestinal e infecção
urinária, acontecendo principalmente se o indivíduo consumir água ou alimentos
contaminados”.
Fonte: KAPER JB, NATARO JP, MOBLEY HLT. Pathogenic Escherichia coli. Nat. Rev. Microbiol., 2: 123-140, 2004
A respeito das bactérias, assinale a alternativa incorreta.
Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 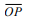 mede
5cm.
mede
5cm.

Sabendo que o segmento 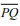 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 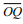 mede:
mede:
Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 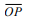 mede
5cm.
mede
5cm.

Sabendo que o segmento 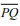 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 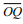 mede:
mede:


Sejam (16,18, 20, ...) e (1/2, 3, 11/2, ...) duas progressões aritméticas. Estas duas progressões
apresentarão somas iguais, para uma mesma quantidade de termos somados, quando o valor
da soma for igual a:


A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g
e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma
nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada
item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:
A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:


Em 1958, como trote para os calouros da universidade de Harvard, nos Estados Unidos, um
grupo de estudantes precisou medir o comprimento da ponte de Harvard (entre Boston e
Cambridge, em Massachusetts), usando como padrão de medida um dos próprios estudantes,
um rapaz chamado Oliver R. Smoot. Após horas de medição, com o estudante deitando-se no
chão e levantando-se sucessivas vezes para as medidas, concluiu-se que a ponte tinha 364,4
smoots, +/- 1 orelha.
A brincadeira fez tanto sucesso e a medição tornou-se tão popular que, na década de 1980, a
ponte foi reformada pela prefeitura, que encomendou blocos de concreto personalizados de 1
smoot de comprimento para a reforma, eternizando as marcações colocadas no solo, que hoje
já constam até no sistema de conversão de medidas da ferramenta Google.
Ainda mais interessante é o fato de que, alguns anos após formado, Oliver Smoot tornou-se
diretor da ANSI, o Instituto Nacional Americano de Padrões (“American National Standards
Institute”) e depois presidente da ISO, a Organização Internacional para Padronização
(“International Organization for Standardization”).
Sabendo que Oliver Smoot tinha 5 pés e 7 polegadas de altura na ocasião da medida,
desprezando o erro de +/- 1 orelha, e assumindo 1 pé = 30,5 cm e 1 polegada = 2,5 cm, o
comprimento da ponte é:


Uma coroa cilíndrica é a região espacial situada entre dois cilindros concêntricos de mesma
altura, um com raio
R
e outro com raio
r
, sendo
r < R
. Se a altura, o volume e a soma das
medidas dos raios dessa coroa cilíndrica são, respectivamente,
4
cm,
4,25π cm3 e
4,25
cm,
então a área total de sua superfície é:


Analise as proposições abaixo.
I – O produto de uma matriz linha por uma matriz linha é uma matriz linha.
II – Uma matriz identidade elevada ao quadrado é uma matriz identidade.
III - O produto de uma matriz por sua transposta é a matriz identidade.
Assinale a alternativa correta.
Analise as proposições abaixo.
I – O produto de uma matriz linha por uma matriz linha é uma matriz linha.
II – Uma matriz identidade elevada ao quadrado é uma matriz identidade.
III - O produto de uma matriz por sua transposta é a matriz identidade.
Assinale a alternativa correta.


A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos
babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz
quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números
procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e
Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:
A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:


Em um triângulo retângulo ABC são construídos três triângulos equiláteros, conforme Figura 1.

Com base na informação e na Figura 1, analise as proposições.
I – A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II – Se a área do triângulo ABC é 6 cm2 e a altura do triângulo CBF é √30cm, então o perímetro
do triângulo ABC é
2 . (4 + √10) cm.
III – Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos
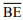 e
e 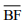 é igual ao comprimento do segmento
é igual ao comprimento do segmento 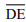 .
.
Assinale a alternativa correta.
Em um triângulo retângulo ABC são construídos três triângulos equiláteros, conforme Figura 1.

Com base na informação e na Figura 1, analise as proposições.
I – A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II – Se a área do triângulo ABC é 6 cm2 e a altura do triângulo CBF é √30cm, então o perímetro do triângulo ABC é 2 . (4 + √10) cm.
III – Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos
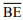 e
e 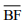 é igual ao comprimento do segmento
é igual ao comprimento do segmento 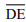 .
.
Assinale a alternativa correta.


O valor de
x . y com x,y 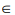 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
O valor de
x . y com x,y 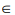 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:


A soma de todas as raízes reais da função ƒ(x) = cotg2 (x) - 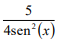 + 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
+ 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
A soma de todas as raízes reais da função ƒ(x) = cotg2 (x) - 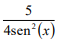 + 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
+ 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:


Considere o prisma triangular com 8 u.c. de altura e a base sendo um triângulo ABC cujos
vértices são os pontos de interseção das retas
2y = x, y + x = 3 e y =ax, com a  . Se o
volume desse prisma triangular é 12 u.v., o valor da soma das abscissas dos vértices do
triângulo ABC é:
. Se o
volume desse prisma triangular é 12 u.v., o valor da soma das abscissas dos vértices do
triângulo ABC é:
 . Se o
volume desse prisma triangular é 12 u.v., o valor da soma das abscissas dos vértices do
triângulo ABC é:
. Se o
volume desse prisma triangular é 12 u.v., o valor da soma das abscissas dos vértices do
triângulo ABC é: 

A função quadrática cujo gráfico contém os pontos (0,-9), (1,0) e (2,15) tem vértice em:

