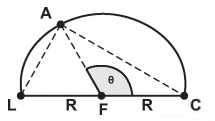
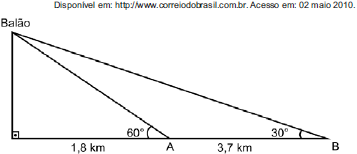
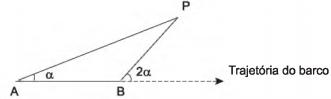
Uma indústria recortou uma placa de metal no
formato triangular ABC, conforme Figura 1, com lados
18, 14 e 12 cm.
Posteriormente, a peça triangular ABC foi dobrada,
de tal maneira que o vértice B ficou sobre o segmento  , e o segmento
, e o segmento  ficou paralelo ao lado
ficou paralelo ao lado  , conforme
Figura 2.
, conforme
Figura 2.

Sabe-se que, na Figura 1, o ângulo AĈB é menor que
o ângulo CÂB e este é menor que o ângulo  , e que
os cortes e dobraduras foram executados corretamente
pelas máquinas.
, e que
os cortes e dobraduras foram executados corretamente
pelas máquinas.
Nessas condições, qual é o valor da soma dos
comprimentos, em centímetro, dos segmentos  e
e  ?
?
Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18, 14 e 12 cm.
Posteriormente, a peça triangular ABC foi dobrada,
de tal maneira que o vértice B ficou sobre o segmento  , e o segmento
, e o segmento  ficou paralelo ao lado
ficou paralelo ao lado  , conforme
Figura 2.
, conforme
Figura 2.

Sabe-se que, na Figura 1, o ângulo AĈB é menor que
o ângulo CÂB e este é menor que o ângulo  , e que
os cortes e dobraduras foram executados corretamente
pelas máquinas.
, e que
os cortes e dobraduras foram executados corretamente
pelas máquinas.
Nessas condições, qual é o valor da soma dos
comprimentos, em centímetro, dos segmentos  e
e  ?
?