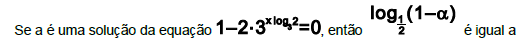Questõessobre Logaritmos
A quantidade de combustível, em litros, existente em um depósito para o funcionamento de um motor
responsável pelo aquecimento de um conjunto de piscinas, em um determinado tempo t (minutos), é dada
por Q(t) = 12 + log3(81 − kt
2), onde t ∈ [0, 20].
Considerando que esse motor funcionou por 20 minutos e que, nesse período de tempo, consumiu 2 litros
de combustível, assinale a alternativa que apresenta, corretamente, o valor de k.
Um biomédico está pesquisando uma espécie de
bactéria descoberta recentemente. Ele assume que o
crescimento da colônia de bactérias ocorre
esponencialmente, ou seja, que o número de bactérias
na colônia será de N0∙ert, passadas t horas do instante
inicial (t = 0), com N0 sendo o número de bactérias no
instante inicial e r a taxa de crescimento, dada em
bactérias por hora. Se, no instante inicial, temos 100
bactérias e, passada meia hora, o número de bactérias
era 450, qual o valor de r? Dado: use a aproximação ln
(4,5) ≈ 1,50.
Se log 2 = x e log 3 = y, então log 288 é
Dados preliminares da pandemia do Covid-19 indicam que,
no início da disseminação, em determinada região, o
número de pessoas contaminadas dobrava a cada 3 dias.
Usando que log10 2 ≈ 0,3 e log10 5 ≈ 0,7, após o primeiro
contágio, o número de infectados atingirá a marca de 4 mil
entre
Considere a sequência 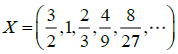 . Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
. Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
Considere a sequência 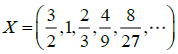 . Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
. Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
Desenvolvida em 1935 por Charles F. Richter, com a colaboração de Beno Gutenberg, a escala Richter permite determinar a magnitude (M) de um terremoto, fenômeno que libera
uma grande quantidade de energia (E) que se propaga pela
Terra em todas as direções. A magnitude e a energia de um
terremoto podem ser relacionadas pela expressão a seguir,
em que E é expressa em erg, uma unidade de medida de
energia do sistema CGS.
logE = 11,8 + 1,5M
A tabela apresenta os efeitos gerados por um terremoto, de
acordo com sua magnitude na escala Richter:

No dia 6 de janeiro de 2020, o sul de Porto Rico foi atingido por um terremoto que liberou uma quantidade de energia
E = 1013,8 J. Considerando a tabela e que 1 erg = 10–7
J, esse
terremoto

A Lei de Zipf, batizada com o nome do linguista
americano George Zipf, é uma lei empírica que
relaciona a frequência (f) de uma palavra em um
dado texto com o seu ranking (r). Ela é dada por
f = A/ rB
O ranking da palavra é a sua posição ao ordenar
as palavras por ordem de frequência. Ou seja, r = 1
para a palavra mais frequente, r = 2 para a segunda
palavra mais frequente e assim sucessivamente, A e B
são constantes positivas.
Disponível em: http://klein.sbm.org.br. Acesso em: 12 ago. 2020 (adaptado).
Com base nos valores de X = log (r) e Y = log (f), é
possível estimar valores para A e B.
No caso hipotético em que a lei é verificada exatamente,
a relação entre Y e X é
Leia o texto e observe a imagem a seguir.
No Brasil, a preservação natural de um cadáver
é rara devido ao clima tropical e ao solo ácido,
que aceleram a sua decomposição. Por isso, a
múmia encontrada em Goianá, Minas Gerais, no
século XIX é tão incomum.
Adaptado de: www.museunacional.ufrj.br

Passados t anos após a morte deste ser humano, suponha que a massa m(t) de seu cadáver, medida em quilogramas, seja dada por m(t) = 40e−C·t, onde e > 1
é uma constante e C é um parâmetro relacionado
às características morfoclimáticas da região onde originalmente se encontrava. Admitindo que passados
t = 600 anos a múmia possuía exatos 4 kg, assinale
a alternativa que apresenta, corretamente, o valor do
parâmetro C.
Leia o texto e observe a imagem a seguir.
No Brasil, a preservação natural de um cadáver é rara devido ao clima tropical e ao solo ácido, que aceleram a sua decomposição. Por isso, a múmia encontrada em Goianá, Minas Gerais, no século XIX é tão incomum.
Adaptado de: www.museunacional.ufrj.br

Passados t anos após a morte deste ser humano, suponha que a massa m(t) de seu cadáver, medida em quilogramas, seja dada por m(t) = 40e−C·t, onde e > 1
é uma constante e C é um parâmetro relacionado
às características morfoclimáticas da região onde originalmente se encontrava. Admitindo que passados
t = 600 anos a múmia possuía exatos 4 kg, assinale
a alternativa que apresenta, corretamente, o valor do
parâmetro C.
Se log2 y = -1/2 + 2/3 log2 x , para x > 0, então
y =
y =
y =
y =
y =
Uma quantidade fixa de um gás ideal é mantida a
temperatura constante, e seu volume varia com o tempo de
acordo com a seguinte fórmula:
V(t) = log2(5 + 2sen(πt)), 0 ≤ t ≤ 2,
em que t é medido em horas e V(t) é medido em m3
. A
pressão máxima do gás no intervalo de tempo [0,2] ocorre
no instante
Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula:
V(t) = log2(5 + 2sen(πt)), 0 ≤ t ≤ 2,
em que t é medido em horas e V(t) é medido em m3 . A pressão máxima do gás no intervalo de tempo [0,2] ocorre no instante
Um lago usado para abastecer uma cidade foi contaminado após um acidente
industrial, atingindo o nível de toxidez T0, correspondente a dez vezes o nível inicial.
Leia as informações a seguir.
• A vazão natural do lago permite que 50% de seu volume sejam renovados a cada dez dias.
• O nível de toxidez T(x), após x dias do acidente, pode ser calculado por meio da seguinte
equação:
T[x] = T0 . [0,5]0,1x
Considere D o menor número de dias de suspensão do abastecimento de água, necessário para que
a toxidez retorne ao nível inicial. Sendo log 2 = 0,3, o valor de D é igual a:
Dadas as funções (fx ) =22x e (gx) =5x , para que valor de x ocorre
a relação f[g(x)]=g[f(x)]?
Use, se necessário, a tabela abaixo:
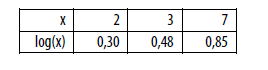

O valor da expressão  é:
é:
O valor da expressão é:
19
Considerando que log10 2 = α e que log10 3 = β, calcule o valor de log9
5
Considerando que log10 2 = α e que log10 3 = β, calcule o valor de log9 5




Em junho de 2016, um terremoto de magnitude 6.0 atingiu a costa leste do
Japão, e, em abril de 2014, um terremoto de magnitude 8.0 atingiu a costa do
Chile. A intensidade dos terremotos foi mensurada usando a escala Richter,
desenvolvida por Charles Richter e Beno Gutenberg. A magnitude (graus) é o
logarítmo das amplitudes (medidas por aparelhos denominados sismógrafos)
das ondas produzidas pela liberação de energia do terremoto. A fórmula utilizada é

onde M é a magnitude, A é a amplitude máxima e A0
é uma amplitude de referência. Usando a fórmula acima, podemos afirmar que as ondas do terremoto
de 2014 foram mais intensas do que em 2016

A escala Richter corresponde ao logaritmo da medida da amplitude das ondas sísmicas a 100 km do epicentro do
terremoto. A intensidade I de um terremoto, medido nesta escala, é um número que varia de 1 = 0 até 1 = 9,5. 1 é
dado pela fórmula: 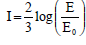 onde E é a energia liberada no terremoto em quilowatt-hora e E0 = 7 x 10-3
kWh. A energia liberada em um dos recentes terremotos do Japão, de intensidade 9 na escala Richter, foi de:
onde E é a energia liberada no terremoto em quilowatt-hora e E0 = 7 x 10-3
kWh. A energia liberada em um dos recentes terremotos do Japão, de intensidade 9 na escala Richter, foi de:
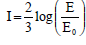 onde E é a energia liberada no terremoto em quilowatt-hora e E0 = 7 x 10-3
kWh. A energia liberada em um dos recentes terremotos do Japão, de intensidade 9 na escala Richter, foi de:
onde E é a energia liberada no terremoto em quilowatt-hora e E0 = 7 x 10-3
kWh. A energia liberada em um dos recentes terremotos do Japão, de intensidade 9 na escala Richter, foi de: Falta de fiscalização e manutenção motivam
baixa durabilidade de estradas
A falta de recursos para obras de construção, fiscalização e manutenção é a principal causa da baixa durabilidade das rodovias brasileiras, aponta estudo da Confederação Nacional do Transporte (CNT).
O desgaste, diz o estudo, é a principal deficiência encontrada no pavimento das estradas brasileiras sob gestão pública e cresceu nos últimos
anos: entre 2004 e 2016, o percentual de trechos desgastados passou de
13% para 49%.
(https://g1.globo.com/economia/noticia/falta-de-fiscalizacao-e-manutencaosao-principais-causas-da-baixa-durabilidade-de-estradas-no-brasil.ghtml)
A partir de um estudo feito sobre os trechos desgastados de uma determinada estrada, cuja extensão total é de 1.000 quilômetros, concluiu-se que o desgaste vem aumentando a uma taxa de 11,7% ao ano
desde 2004, ano em que foi observado 130 quilômetros de desgaste.
Supondo que essa taxa se mantenha constante nos próximos anos,
está correto afirmar que esta estrada estará totalmente desgastada no
ano de:
Dados: log(1,117) = 0,05; log(13) = 1,1
A falta de recursos para obras de construção, fiscalização e manutenção é a principal causa da baixa durabilidade das rodovias brasileiras, aponta estudo da Confederação Nacional do Transporte (CNT).
Num instante t=0, um recipiente contém uma quantidade Qo de bactérias que se
reproduzem normalmente. Em um instante t>0 a quantidade de bactérias
existentes nesse recipiente é dada pela fórmula, Q(t) = Qo.e
at, onde t é o tempo, a
é a constante que depende do tipo de bactéria e e é o número neperiano que é a
base do logaritmo natural. Supondo que um cultivo inicial de 10 bactérias se
reproduz em condições favoráveis e que doze horas mais tarde contamos 50
bactérias nesse cultivo, qual o valor da constante a para este tipo de bactéria?
Obs. o símbolo ln, abaixo, representa o logaritmo natural, ou seja, o logaritmo na
base e