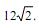Analise a figura abaixo.
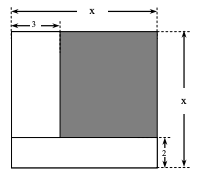
A partir das informações da figura, marque V para as
afirmativas verdadeiras e F para as falsas.
( ) A medida da área sombreada em função de x, denotada
por A(x), pode ser expressa pela função quadrática
A(x) = x2
– 5x + 6.
( ) Não se pode atribuir valores para x no intervalo aberto
]2, 3[.
( ) O gráfico da função quadrática que representa a
medida da área sombreada intercepta o eixo das
ordenadas no ponto (0,5).
Marque a sequência correta.
Analise a figura abaixo.

A partir das informações da figura, marque V para as afirmativas verdadeiras e F para as falsas.
( ) A medida da área sombreada em função de x, denotada por A(x), pode ser expressa pela função quadrática A(x) = x2 – 5x + 6.
( ) Não se pode atribuir valores para x no intervalo aberto ]2, 3[.
( ) O gráfico da função quadrática que representa a medida da área sombreada intercepta o eixo das ordenadas no ponto (0,5).
Marque a sequência correta.











 é o lado de um polígono regular inscrito na circunferência de centro O e raio r.
é o lado de um polígono regular inscrito na circunferência de centro O e raio r.