bfbe45d3-b3
UFPR 2015 - Matemática - Funções, Equações Exponenciais
A análise de uma aplicação financeira ao longo do tempo mostrou que a expressão V(t) = 1000.20,0625.t fornece uma
boa aproximação do valor V (em reais) em função do tempo t (em anos), desde o início da aplicação. Depois de quantos
anos o valor inicialmente investido dobrará?
A análise de uma aplicação financeira ao longo do tempo mostrou que a expressão V(t) = 1000.20,0625.t fornece uma
boa aproximação do valor V (em reais) em função do tempo t (em anos), desde o início da aplicação. Depois de quantos
anos o valor inicialmente investido dobrará?
A
8.
B
12.
C
16.
D
24.
E
32.

 em que No é a quantidade inicial, isto é, No = N (0) e k é a constante de proporcionalidade. Se inicialmente havia 5000 bactérias na cultura e 8000 bactérias 10 minutos depois, quanto tempo será necessário para que o número de bactérias se torne duas vezes maior que o inicial?
em que No é a quantidade inicial, isto é, No = N (0) e k é a constante de proporcionalidade. Se inicialmente havia 5000 bactérias na cultura e 8000 bactérias 10 minutos depois, quanto tempo será necessário para que o número de bactérias se torne duas vezes maior que o inicial?



 é contínua.
é contínua.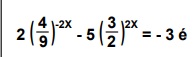
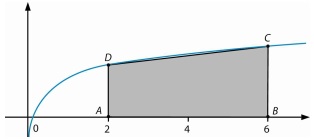


 , com
, com  em horas e N em milhares de micro-organismos.
em horas e N em milhares de micro-organismos. 
 para t ≥ 0 .
para t ≥ 0 .  é maior que o de
é maior que o de  .
. é menor que o de
é menor que o de 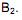 .
. aumenta 10% e o de
aumenta 10% e o de  aumenta 90%.
aumenta 90%. cresce 20 vezes menos que o de
cresce 20 vezes menos que o de  .
.