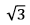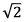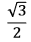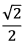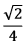Em um experimento sobre orientação e navegação de pombos,considerou-se o pombal como a origem O de um sistema de coordenadas cartesianas e os eixos orientados Sul-Norte (SN) e Oeste-Leste (WL). Algumas aves foram liberadas num ponto P que fica 52 km ao leste do eixo SN e a 30 km ao sul do eixo WL. O ângulo azimutal de P é o ângulo, em graus, medido no sentido horário a partir da semirreta ON até a semirreta OP. No experimento descrito, a distância do pombal até o ponto de liberação das aves, em km, e o ângulo azimutal, em graus, desse ponto são,respectivamente:
Dado: √3604 ≈ 60.

Em um experimento sobre orientação e navegação de pombos,considerou-se o pombal como a origem O de um sistema de coordenadas cartesianas e os eixos orientados Sul-Norte (SN) e Oeste-Leste (WL). Algumas aves foram liberadas num ponto P que fica 52 km ao leste do eixo SN e a 30 km ao sul do eixo WL. O ângulo azimutal de P é o ângulo, em graus, medido no sentido horário a partir da semirreta ON até a semirreta OP. No experimento descrito, a distância do pombal até o ponto de liberação das aves, em km, e o ângulo azimutal, em graus, desse ponto são,respectivamente:
Dado: √3604 ≈ 60.



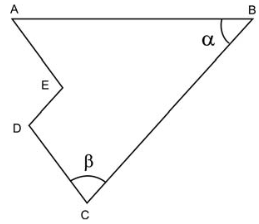
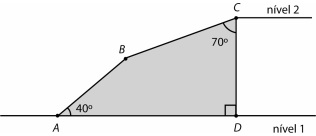
 tangencia os três quadrados. Os lados
tangencia os três quadrados. Os lados 






 , paralelo a
, paralelo a  paralelo a
paralelo a