Questõesde USP sobre Álgebra

InícioTodas as questões
1
1
1
Foram encontradas 14 questões
d86c1813-73
USP 2021 - Matemática - Álgebra, Problemas

Os funcionários de um salão de beleza compraram um presente no valor de R$ 200,00 para a recepcionista do estabelecimento. No momento da divisão igualitária do valor, dois deles desistiram de participar e, por causa disso, cada pessoa que ficou no grupo precisou pagar R$ 5,00 a mais que a quantia originalmente prevista. O valor pago por pessoa que permaneceu na divisão do custo do presente foi:  

A
R$ 10,00
B
R$ 15,00
C
R$ 20,00
D
R$ 25,00
E
R$ 40,00
d86f4b1a-73
USP 2021 - Matemática - Aritmética e Problemas, Álgebra, Problemas

Uma empresa construiu um poço para armazenar água de reúso. O custo para construir o primeiro metro foi de R$ 1.000,00, e cada novo metro custou R$ 200,00 a mais do que o imediatamente anterior. Se o custo total da construção foi de R$ 48.600,00, a profundidade do poço é: 

A
15 m
B
18 m
C
21 m
D
24 m
E
27 m
de7c3618-7b
USP 2021 - Matemática - Álgebra, Problemas

Uma treinadora de basquete aplica o seguinte sistema de pontuação em seus treinos de arremesso à cesta: cada jogadora recebe 5 pontos por arremesso acertado e perde 2 pontos por arremesso errado. Ao fim de 50 arremessos, uma das jogadoras contabilizou 124 pontos. Qual é a diferença entre as quantidades de arremessos acertados e errados dessa jogadora?

A
12
B
14
C
16
D
18
E
20
0d5026a8-99
USP 2019 - Matemática - Álgebra, Pontos e Retas, Geometria Analítica, Equação do 2º Grau e Problemas do 2º Grau

Um ponto (x,y) do plano cartesiano pertence ao conjunto F se é equidistante dos eixos ܱܺ0X e ܱ0Y e pertence ao círculo de equação x2 + y2 - 2x - 6y +2 = 0. É correto afirmar que F

A
é um conjunto vazio.
B
tem exatamente 2 pontos, um no primeiro quadrante e outro no segundo quadrante.
C
tem exatamente 2 pontos, ambos no primeiro quadrante.
D
tem exatamente 3 pontos, sendo dois no primeiro quadrante e outro no segundo quadrante.
E
tem exatamente 4 pontos, sendo dois no primeiro quadrante e dois no segundo quadrante.
0d4ba3d7-99
USP 2019 - Matemática - Álgebra, Problemas

Uma agência de turismo vendeu um total de 78 passagens para os destinos: Lisboa, Paris e Roma. Sabe‐se que o número de passagens vendidas para Paris foi o dobro do número de passagens vendidas para os outros dois destinos conjuntamente. Sabe‐se também que, para Roma, foram vendidas duas passagens a mais que a metade das vendidas para Lisboa. Qual foi o total de passagens vendidas, conjuntamente, para Paris e Roma?

A
26
B
38
C
42
D
62
E
68
0d44750c-99
USP 2019 - Matemática - Álgebra, Equação do 2º Grau e Problemas do 2º Grau

Se 3x2 - 9x + 7 = (x - a)3 - (x - b)3, para todo número real x, o valor de ܽa + b é

A
3.
B
5.
C
6.
D
9.
E
12.
0d37255f-99
USP 2019 - Matemática - Álgebra, Problemas

A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais. Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?

A
R$ 2.000,00
B
R$ 3.200,00
C
R$ 3.600,00
D
R$ 4.000,00
E
R$ 4.800,00
d117368e-f2
USP 2018 - Matemática - Álgebra, Problemas

Forma‐se uma pilha de folhas de papel, em que cada folha tem 0,1 mm de espessura. A pilha é formada da seguinte maneira: coloca‐se uma folha na primeira vez e, em cada uma das vezes seguintes, tantas quantas já houverem sido colocadas anteriormente. Depois de 33 dessas operações, a altura da pilha terá a ordem de grandeza

A
da altura de um poste.
B
da altura de um prédio de 30 andares.
C
do comprimento da Av. Paulista.
D
da distância da cidade de São Paulo (SP) à cidade do Rio de Janeiro (RJ).
E
do diâmetro da Terra.
d107b661-f2
USP 2018 - Matemática - Aritmética e Problemas, Álgebra, Problemas, Razão, Proporção e Números Proporcionais

Em uma família, o número de irmãs de cada filha é igual à metade do número de irmãos. Cada filho tem o mesmo número de irmãos e irmãs.


O número total de filhos e filhas da família é

A
4
B
5
C
7
D
10
E
15
3361f233-d4
USP 2017 - Matemática - Álgebra, Equação do 2º Grau e Problemas do 2º Grau

Considere o polinômio


                P(x) = xn + αn-1xn-1 +... + α1x + αo .


em que αo , ..., αn-1 ∈ ℝ. Sabe-se que as suas n raízes estão sobre a circunferência unitária e que αo < 0.


O produto das n raízes de P(x), para qualquer inteiro n ≥  1 , é:

A
-1
B
in
C
in+1
D
(-1)n
E
(-1)n+1
003e2cd7-e1
USP 2016 - Matemática - Álgebra, Equação do 2º Grau e Problemas do 2º Grau, Polinômios

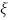O polinômio P(x) = x3 - 3x2 + 7x - 5 possui uma raiz complexa cuja parte imaginária é positiva. A parte real de 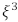é igual a

A
-11
B
-7
C
9
D
10
E
12
5ec03119-97
USP 2015 - Matemática - Álgebra, Radiciação

A igualdade correta para quaisquer a e b , números reais maiores do que zero, é

A


B


C


D


E


5ed0d5b3-97
USP 2015 - Matemática - Aritmética e Problemas, Álgebra, Problemas, Médias

Em uma classe com 14 alunos, 8 são mulheres e 6 são homens. A média das notas das mulheres no final do semestre ficou 1 ponto acima da média da classe. A soma das notas dos homens foi metade da soma das notas das mulheres. Então, a média das notas dos homens ficou mais próxima de

A
4,3
B
4,5
C
4,7
D
4,9
E
5,1
f3414da4-e4
USP 2012 - Matemática - Potenciação, Álgebra

As propriedades aritméticas e as relativas à noção de ordem desempenham um importante papel no estudo dos números reais. Nesse contexto, qual das afirmações abaixo é correta?

A
Quaisquer que sejam os números reais positivos a e b , é verdadeiro que
imagem-069.jpg
B
Quaisquer que sejam os números reais a e b tais que a2 - b2 = 0, é verdadeiro que a = b .
C
Qualquer que seja o número real a , é verdadeiro que imagem-070.jpg
D
Quaisquer que sejam os números reais a e b não nulos tais que a< b , é verdadeiro que 1/ b < 1 / a.
E
Qualquer que seja o número real a, com 0 < a < 1, é verdadeiro que a2 < imagem-071.jpg