Questão f4a764e4-d6
Prova:UNESP 2014
Disciplina:Matemática
Assunto:Números Complexos
Sabe-se que 1 é uma raiz de multiplicidade 3 da equação x5 – 3 · x4 + 4 · x3 – 4 · x2 + 3 · x – 1 = 0. As outras raízes dessa equação, no Conjunto Numérico dos Complexos, são
Sabe-se que 1 é uma raiz de multiplicidade 3 da equação x5 – 3 · x4 + 4 · x3 – 4 · x2 + 3 · x – 1 = 0. As outras raízes dessa equação, no Conjunto Numérico dos Complexos, são
A
(– 1 – i) e (1 + i).
B
(1 – i) 2 .
C
(– i) e (+ i).
D
(– 1) e (+ 1).
E
(1 – i) e (1 + i).
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Aplicando Briot - Ruffini e sabendo que o 1 é uma raíz de multiplicidade 3:
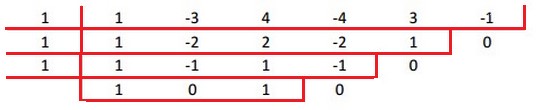
Assim, as outras raízes são as raízes da equação x² + 1 = 0. Logo, x = i ou x = - i.
Resposta: Alternativa C.

Assim, as outras raízes são as raízes da equação x² + 1 = 0. Logo, x = i ou x = - i.
Resposta: Alternativa C.






