Questão f09ef054-d6
Prova:UNESP 2014
Disciplina:Matemática
Assunto:Quadriláteros, Geometria Plana
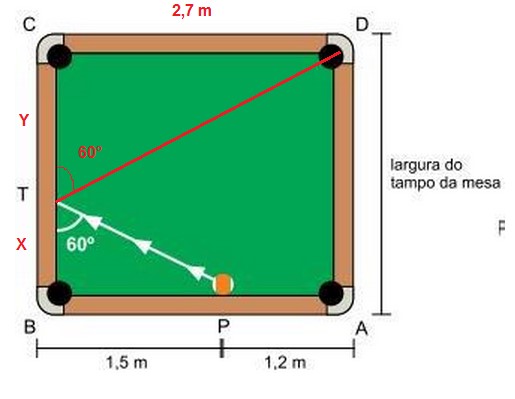
A figura representa a vista superior do tampo plano e ho- rizontal de uma mesa de bilhar retangular ABCD, com caçapas em A, B, C e D. O ponto P, localizado em 
, representa a posição de uma bola de bilhar, sendo PB = 1,5 m e PA = 1,2 m. Após uma tacada na bola, ela se desloca em linha reta colidindo com 
no ponto T, sendo a medida do ângulo 
igual a 60°. Após essa colisão, a bola segue, em trajetória reta, diretamente até a caçapa D.
Nas condições descritas e adotando √3 = 1,73 , a largura do tampo da mesa, em metros, é próxima de
A figura representa a vista superior do tampo plano e ho- rizontal de uma mesa de bilhar retangular ABCD, com caçapas em A, B, C e D. O ponto P, localizado em , representa a posição de uma bola de bilhar, sendo PB = 1,5 m e PA = 1,2 m. Após uma tacada na bola, ela se desloca em linha reta colidindo com no ponto T, sendo a medida do ângulo igual a 60°. Após essa colisão, a bola segue, em trajetória reta, diretamente até a caçapa D.
Nas condições descritas e adotando √3 = 1,73 , a largura do tampo da mesa, em metros, é próxima de
, representa a posição de uma bola de bilhar, sendo PB = 1,5 m e PA = 1,2 m. Após uma tacada na bola, ela se desloca em linha reta colidindo com no ponto T, sendo a medida do ângulo igual a 60°. Após essa colisão, a bola segue, em trajetória reta, diretamente até a caçapa D.Nas condições descritas e adotando √3 = 1,73 , a largura do tampo da mesa, em metros, é próxima de
A
2,42.
B
2,08.
C
2,28.
D
2,00.
E
2,56.
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Desenhando a figura abaixo:
Encontrando X:
TgΘ = senΘ/cosΘ
Tg60 = 1,5/X
√3 = 1,73 = 1,5/X
X = 1,5/1,73
X ≅ 0,86
Encontrando Y:
TgΘ = senΘ/cosΘ
Tg60 = 2,7/Y
√3 = 1,73 = 2,7/Y
Y = 2,7/1,73
Y ≅ 1,56
Assim: X + Y = 0,87 + 1,56 ≅ 2,42 m
Resposta: Alternativa A.
Encontrando X:
TgΘ = senΘ/cosΘ
Tg60 = 1,5/X
√3 = 1,73 = 1,5/X
X = 1,5/1,73
X ≅ 0,86
Encontrando Y:
TgΘ = senΘ/cosΘ
Tg60 = 2,7/Y
√3 = 1,73 = 2,7/Y
Y = 2,7/1,73
Y ≅ 1,56
Assim: X + Y = 0,87 + 1,56 ≅ 2,42 m
Resposta: Alternativa A.
