Em um recipiente com a forma de um paralelepípedo retângulo com 40 cm de comprimento, 25 cm de largura e 20 cm de altura, foram depositadas, em etapas, pequenas esferas, cada uma com volume igual a 0,5 cm3 . Na primeira etapa, depositou-se uma esfera; na segunda, duas; na terceira, quatro; e assim sucessivamente, dobrando-se o número de esferas a cada etapa.
Admita que, quando o recipiente está cheio, o espaço vazio entre as esferas é desprezível. Considerando 210 = 1000, o menor número de etapas necessárias para que o volume total de esferas seja maior do que o volume do recipiente é:
Admita que, quando o recipiente está cheio, o espaço vazio entre as esferas é desprezível. Considerando 210 = 1000, o menor número de etapas necessárias para que o volume total de esferas seja maior do que o volume do recipiente é:
Gabarito comentado
Vamos começar desenhando a figura descrita no enunciado:
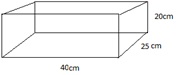
Assim o volume do paralelepípedo será Vp= 20x25x40x = 20000cm3
De acordo com o enunciado, podemos representar o volume total das esferas do seguinte modo:
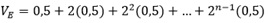
colocando o 0,05 em evidência:
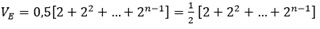
Reparem que dentro dos colchetes, temos uma soma finita de uma PG, onde a1 = 1 e q = 2
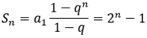
Logo,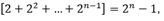 
Substituindo
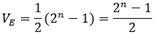
Como Ve > Vp
Então, resolvendo a equação exponencial acima encontramos n ≥ 16
Letra B
