Questão d0429614-7c
Prova:ENEM 2014
Disciplina:Matemática
Assunto:Raciocínio Lógico, Quadriláteros, Geometria Plana
Uma pessoa possui um espaço retangular de lados 11,5 m e 14 m no quintal de sua casa e pretende fazer um pomar doméstico de maçãs. Ao pesquisar sobre o plantio dessa fruta, descobriu que as mudas de maçã devem ser plantadas em covas com uma única muda e com espaçamento mínimo de 3 metros entre elas e entre elas e as laterais do terreno. Ela sabe que conseguirá plantar um número maior de mudas em seu pomar se dispuser as covas em filas alinhadas paralelamente ao lado de maior extensão.
O número máximo de mudas que essa pessoa poderá plantar no espaço disponível é
Uma pessoa possui um espaço retangular de lados 11,5 m e 14 m no quintal de sua casa e pretende fazer um pomar doméstico de maçãs. Ao pesquisar sobre o plantio dessa fruta, descobriu que as mudas de maçã devem ser plantadas em covas com uma única muda e com espaçamento mínimo de 3 metros entre elas e entre elas e as laterais do terreno. Ela sabe que conseguirá plantar um número maior de mudas em seu pomar se dispuser as covas em filas alinhadas paralelamente ao lado de maior extensão.
O número máximo de mudas que essa pessoa poderá plantar no espaço disponível é
O número máximo de mudas que essa pessoa poderá plantar no espaço disponível é
A
4.
B
8.
C
9.
D
12 .
E
20.
Gabarito comentado
Vinícius WerneckMatemático e Doutor em Geofísica.
Pelo enunciado, sabemos que as mudas terão que ficar a uma distância de 3 metros das laterais, logo:
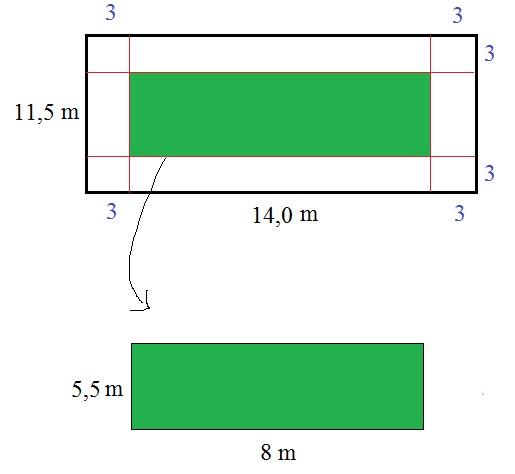
Agora, temos que espaçar o máximo de sementes com no mínimo 3 metros de distância uma da outra, como demostra a figura abaixo:
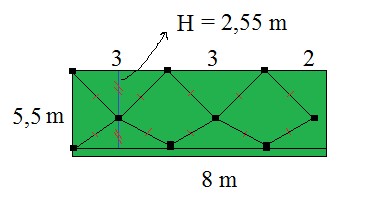
Assim, temos um triângulo equilátero, onde H é a altura do triângulo, o mesmo é calculado para sabermos se cabe mais uma fileira no retângulo, assim:
H = L*√ 3 / 2
H = (3 * 1,7) / 2
H = 2,55 m
Logo, somando 2,55 + 2,55 temos 5,1 m, ou seja, cabe mais uma fileira no retângulo, como foi de fato construído no desenho acima. Assim, completamos essa fileira com mais 3 sementes, tem-se um total de 9 sementes.
Resposta: Alternativa C.

Agora, temos que espaçar o máximo de sementes com no mínimo 3 metros de distância uma da outra, como demostra a figura abaixo:

Assim, temos um triângulo equilátero, onde H é a altura do triângulo, o mesmo é calculado para sabermos se cabe mais uma fileira no retângulo, assim:
H = L*√ 3 / 2
H = (3 * 1,7) / 2
H = 2,55 m
Logo, somando 2,55 + 2,55 temos 5,1 m, ou seja, cabe mais uma fileira no retângulo, como foi de fato construído no desenho acima. Assim, completamos essa fileira com mais 3 sementes, tem-se um total de 9 sementes.
Resposta: Alternativa C.






