A figura foi extraída de um antigo jogo para computadores, chamado Bang! Bang!
No jogo, dois competidores controlam os canhões A e B, disparando balas
alternadamente com o objetivo de atingir o canhão do adversário; para isso, atribuem
valores estimados para o módulo da velocidade inicial de disparo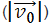 
e para o ângulo
de disparo (θ).
Em determinado momento de uma partida, o competidor B deve disparar; ele sabe
que a bala disparada anteriormente, θ = 53°, passou tangenciando o ponto P.
No jogo,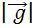 
é igual a 10 m/s2 . Considere sen 53° = 0,8, cos 53° = 0,6 e desprezível
a ação de forças dissipativas.
Disponível em: http://mebdownloads.butzke.net.br. Acesso em: 18 abr. 2015 (adaptado).
Com base nas distâncias dadas e mantendo o último ângulo de disparo, qual deveria ser,
aproximadamente, o menor valor de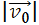 
que permitiria ao disparo efetuado pelo canhão
B atingir o canhão A?
A figura foi extraída de um antigo jogo para computadores, chamado Bang! Bang!
No jogo, dois competidores controlam os canhões A e B, disparando balas
alternadamente com o objetivo de atingir o canhão do adversário; para isso, atribuem
valores estimados para o módulo da velocidade inicial de disparo 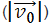e para o ângulo
de disparo (θ).
Em determinado momento de uma partida, o competidor B deve disparar; ele sabe que a bala disparada anteriormente, θ = 53°, passou tangenciando o ponto P.
No jogo, 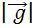é igual a 10 m/s2 . Considere sen 53° = 0,8, cos 53° = 0,6 e desprezível
a ação de forças dissipativas.
Disponível em: http://mebdownloads.butzke.net.br. Acesso em: 18 abr. 2015 (adaptado).
Com base nas distâncias dadas e mantendo o último ângulo de disparo, qual deveria ser,
aproximadamente, o menor valor de 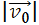que permitiria ao disparo efetuado pelo canhão
B atingir o canhão A?
Gabarito comentado
