Considere os números reais a, b e c, que
fazem com que as sequências S1 = (2c, a, 7a), S2 = (b, c, 2c - 1) e S3 = (4b, a - c, - 2c) sejam três progressões
aritméticas de razões r1 , r2 e r3 ,
respectivamente. Então a sequência S = (r1, r2, r3) é uma progressão:
Considere os números reais a, b e c, que fazem com que as sequências S1 = (2c, a, 7a), S2 = (b, c, 2c - 1) e S3 = (4b, a - c, - 2c) sejam três progressões aritméticas de razões r1 , r2 e r3 , respectivamente. Então a sequência S = (r1, r2, r3) é uma progressão:
 mede 2 cm e os ângulos
mede 2 cm e os ângulos  e
e  medem, respectivamente,
60º
e
75º
, então a
área e o perímetro deste triângulo são,
respectivamente:
medem, respectivamente,
60º
e
75º
, então a
área e o perímetro deste triângulo são,
respectivamente:

 é 1/7.
é 1/7. e D =
e D =  então (C
então (C .
. = 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3.
= 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3. 
 mede 10 cm, a área do trapézio é:
mede 10 cm, a área do trapézio é: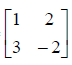 e B =
e B = 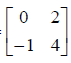 .
.