5424c783-67
UEG 2007 - Matemática - Aritmética e Problemas, Álgebra, Sistemas de Numeração e Operações Fundamentais, Problemas
Paulo disse a Maria que iria descobrir o seu número de telefone. Pediu-lhe que, em segredo, multiplicasse o número constituído pelos quatro primeiros algarismos de seu telefone por 40 e a esse produto adicionasse 1. Pediu-lhe, então, que multiplicasse o número obtido por 250 e, em seguida, somasse o resultado disso ao número formado pelos quatro últimos algarismos de seu telefone. Paulo afirmou que o número do telefone seria este resultado. Infelizmente, o número estava errado, pois para obter o número correto deveria subtrair certa quantidade deste resultado. Esta quantidade é
Paulo disse a Maria que iria descobrir o seu número de telefone. Pediu-lhe que, em segredo, multiplicasse o número constituído pelos quatro primeiros algarismos de seu telefone por 40 e a esse produto adicionasse 1. Pediu-lhe, então, que multiplicasse o número obtido por 250 e, em seguida, somasse o resultado disso ao número formado pelos quatro últimos algarismos de seu telefone. Paulo afirmou que o número do telefone seria este resultado. Infelizmente, o número estava errado, pois para obter o número correto deveria subtrair certa quantidade deste resultado. Esta quantidade é
A
350.
B
250.
C
150.
D
100.


 é igual a
é igual a


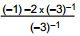 é igual a:
é igual a: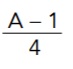 .
.

 é igual a 1 dividido por
é igual a 1 dividido por