Questõessobre Progressão Aritmética - PA

InícioTodas as questões
1
1
Foram encontradas 211 questões
7b78452a-5f
UERJ 2011 - Matemática - Raciocínio Lógico, Progressão Aritmética - PA, Progressões

Um cliente, ao chegar a uma agência bancária, retirou a última senha de atendimento do dia, com o número 49. Verificou que havia 12 pessoas à sua frente na fila, cujas senhas representavam uma progressão aritmética de números naturais consecutivos, começando em 37.

Algum tempo depois, mais de 4 pessoas desistiram do atendimento e saíram do banco. Com isso, os números das senhas daquelas que permaneceram na fila passaram a formar uma nova progressão aritmética.

Se os clientes com as senhas de números 37 e 49 não saíram do banco, o número máximo de pessoas que pode ter permanecido na fila é:

A
6
B
7
C
9
D
12
bd358417-31
UERJ 2016, UERJ 2016 - Matemática - Progressão Aritmética - PA, Progressões

Um fisioterapeuta elaborou o seguinte plano de treinos diários para o condicionamento de um maratonista que se recupera de uma contusão:

• primeiro dia - corrida de 6 km;

• dias subsequentes - acréscimo de 2 km à corrida de cada dia imediatamente anterior.

O último dia de treino será aquele em que o atleta correr 42 km.

O total percorrido pelo atleta nesse treinamento, do primeiro ao último dia, em quilômetros, corresponde a:

A
414
B
438
C
456
D
484
086a01c0-1d
PUC - RS 2015 - Matemática - Progressão Aritmética - PA, Progressões

Considere as sequências numéricas

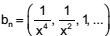an = ( 3x – 9, 4x – 9, 5x – 9, ...) e onde n ≥ 1. Se a4 = b4 , então o valor de x é igual a

A
0
B
1
C
2
D
3
E
4
768377da-e2
FATEC 2011 - Matemática - Progressão Aritmética - PA, Funções, Logaritmos, Polinômios, Progressões

Considere a equação polinomial x3 − 9x2 + kx + 21 = 0, com k real. Se suas raízes estão em progressão aritmética, o valor de log2 (3k − 1)2 é

A
8.
B
10.
C
12.
D
16.
E
20.
47632cfd-73
UDESC 2011 - Matemática - Progressão Aritmética - PA, Trigonometria, Progressões

Considere x ∈ ( 0,π/2) o valor que faz com que os termos sen(x) , 2cos( 2x) e 3sen (x ) formem, nessa ordem, uma progressão aritmética.
A soma dos três termos dessa progressão é igual a:

A
 3
B
1/2
C
π/3
D
 π/6
E
 -3 +3√3
4a51cea2-a4
UNESP 2015 - Matemática - Progressão Aritmética - PA, Progressões

A figura indica o padrão de uma sequência de grades, feitas com vigas idênticas, que estão dispostas em posição horizontal e vertical. Cada viga tem 0,5 m de comprimento. O padrão da sequência se mantém até a última grade, que é feita com o total de 136,5 metros lineares de vigas.

                         

O comprimento do total de vigas necessárias para fazer a sequência completa de grades, em metros, foi de


A
4877.
B
4640.
C
4726.
D
5195.
E
5162.
e9798374-94
UNESP 2011 - Matemática - Progressão Aritmética - PA, Equações Polinomiais, Progressões

Dado que as raízes da equação x3 – 3x2 – x + k = 0, onde k é uma constante real, formam uma progressão aritmética, o valor de k é:

A
– 5.
B
– 3.
C
0.
D
3.
E
5.
82abf0a8-97
FGV 2015 - Matemática - Progressão Aritmética - PA, Progressões

Os números nas seis faces de um cubo são seis múltiplos consecutivos de 3. Além disso, as somas dos números em faces opostas são todas iguais. A figura, a seguir, mostra três faces com os números 18, 24 e 27.  

                                              

A soma dos três números que estão nas faces ocultas do cubo é  


A
66.
B
72.
C
84.
D
36.
E
48.
d4e1b5ee-96
CEDERJ 2013 - Matemática - Progressão Aritmética - PA, Progressões

Um aluno começou a construir, com palitos, uma sequência de retângulos justapostos em uma fileira horizontal. A figura, a seguir, mostra os três primeiros termos dessa sequência:

                                      P1: 

                                      P2:  

                                      P3: 

O primeiro termo da sequência, P1, foi construído com 4 palitos; o segundo, P2, com 7 palitos; o terceiro, P3, com 10 palitos; e assim por diante, isto é, ao enésimo termo da sequência, Pn , acrescenta-se mais um retângulo, utilizando-se um número mínimo de palitos, para formar o termo seguinte, Pn+1. Para construir o vigésimo termo desta sequência, P20, o aluno precisará de

A
60 palitos.
B
61 palitos.
C
80 palitos.
D
81 palitos.
00188296-39
PUC - PR 2014 - Matemática - Progressão Aritmética - PA, Progressões

Um consumidor, ao adquirir um automóvel, assumiu um empréstimo no valor total de R$ 42.000,00 (já somados juros e encargos). Esse valor foi pago em 20 parcelas, formando uma progressão aritmética decrescente. Dado que na segunda prestação foi pago o valor de R$ 3.800,00, a razão desta progressão aritmética é:

A
– 300.
B
– 200.
C
– 150.
D
– 100.
E
– 350.
01dca108-40
UECE 2013 - Matemática - Progressão Aritmética - PA, Progressões

Seja ( x1, x2, x3, ... ) uma progressão aritmética cujo quarto termo é igual a 6,5 e o oitavo termo igual a 15,5. Se f: R→ R é a função definida por f(x) = 3x – 1 e para, cada n, definirmos yn = f(xn), então a soma y1 + y2 + y3 + ... + y16 é igual a

A
782.
B
648.
C
540.
D
419.
fbdc2eb8-3b
USP 2014 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Progressões



Dadas as sequências αn = n2 + 4n + 4 , bn =    , cn = αn+1 - αn  e  dn = bn+1/bn , definidas para valores inteiros  positivos de n, considere as seguintes afirmações:

I. ܽαn é uma progressão geométrica;

II. ܾbn é uma progressão geométrica;

III. ܿcn é uma progressão aritmética;

IV. ݀dn é uma progressão geométrica.

São verdadeiras apenas


A
I, II e III.
B
I, II e IV.
C
I e III.
D
II e IV.
E
III e IV.
919cf12b-3c
PUC - RJ 2014 - Matemática - Progressão Aritmética - PA, Progressões

Os números a1 = 5x - 5, a2 = x + 14 e a3 = 6x - 3 estão em PA.

A soma dos 3 números é igual a:

A
48
B
54
C
72
D
125
E
130
d31c16b6-3b
PUC - RJ 2013 - Matemática - Progressão Aritmética - PA, Progressões

A soma de todos os números naturais pares de três algarismos é:

A
244888
B
100000
C
247050
D
204040
E
204000
3ce19cbb-f4
IF-BA 2013 - Matemática - Progressão Aritmética - PA, Progressões

Numa estrada retilínea, serão instalados oito postos de atendimento P0, P1, P2, ..., P7, nesta ordem, e igualmente espaçados. Os postos extremos são P0 e P7, cujas marcas estão nos quilômetros 213 e 332, respectivamente. Sendo assim, o quinto posto da estrada estará no quilômetro

A
256
B
272,5
C
281
D
287,5
E
298
740a8cf3-d5
UNICAMP 2014 - Matemática - Progressão Aritmética - PA, Progressões

Se ( a1, a2,…, a13) é uma progressão aritmética (PA) cuja soma dos termos é 78, então a7 é igual a

A
6.
B
7.
C
8.
D
9.
6cca69af-ac
PUC-MINAS 2014 - Matemática - Progressão Aritmética - PA, Progressões

A sistematização das notas musicais permitiu a padronização de instrumentos e, com isso, a universalização da composição musical desde o período renascentista. O método adotado para a criação de notas foi o de construir uma sequência de frequências de sons conforme uma progressão geométrica de razão q. Um músico adota a frequência de Lá (1º. termo) em 440Hz e, após doze intervalos, obtém o próximo Lá (13º. termo) em 880Hz , como apresentado na tabela a seguir.

imagem-007.jpg

Se esse músico deseja afinar seu instrumento utilizando a frequência da nota Fá, nono termo dessa escala, a frequência que ele deverá usar, em hertz, é igual a:

A
440imagem-008.jpg
B
440imagem-009.jpg
C
440imagem-010.jpg
D
440imagem-011.jpg
8d47d750-ab
UEA 2014 - Matemática - Progressão Aritmética - PA, Progressões

O preço de um litro de óleo de copaíba aumentou de R$ 30,00, em 2009, para R$ 134,00, em 2013. Supondo que o aumento do preço, ano a ano, tenha ocorrido em progressão aritmética e que este aumento se mantenha na mesma razão nos próximos anos, é correto afirmar que o preço de um litro de óleo de copaíba estará aproximadamente 600% maior do que o preço de 2009, no ano de

A
2014.
B
2015.
C
2016.
D
2017.
E
2018.
33ed74bd-a6
UECE 2011 - Matemática - Progressão Aritmética - PA, Progressões

O maior valor da razão de uma progressão aritmética para que os números 7, 23 e 43 sejam três de seus termos é

A
4.
B
16.
C
2.
D
8.
e086540c-f0
UNICAMP 2013 - Matemática - Progressão Aritmética - PA, Quadriláteros, Geometria Plana, Progressões

O perímetro de um triângulo retângulo é igual a 6,0 m e as medidas dos lados estão em progressão aritmética (PA). A área desse triângulo é igual a

A
3,0 m2 .
B
2,0 m2 .
C
1,5 m2 .
D
3,5 m2 .