cf9340bf-28
UNIFESP 2005 - Matemática - Progressão Aritmética - PA, Progressões
Se os primeiros quatro termos de uma progressão aritmética são a, b, 5a, d, então o quociente d/b é igual a
Se os primeiros quatro termos de uma progressão aritmética são a, b, 5a, d, então o quociente d/b é igual a
A
1/4.
B
1/3.
C
2.
D
7/3.
E
5.
 definida por:
definida por:  se n ≥ 3, n ∈ IN onde IN representa o conjunto dos números naturais. O valor de x para que a soma dos dez primeiros termos desta sequência seja igual a 396 é:
se n ≥ 3, n ∈ IN onde IN representa o conjunto dos números naturais. O valor de x para que a soma dos dez primeiros termos desta sequência seja igual a 396 é: 

 formam, nesta ordem, uma progressão aritmética, com
formam, nesta ordem, uma progressão aritmética, com  então o valor de
então o valor de 
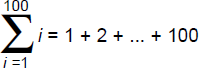




 em anos, pela expressão
em anos, pela expressão