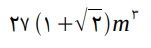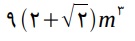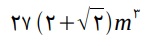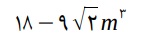09ec85f0-64
UFMG 2006 - Matemática - Áreas e Perímetros, Quadriláteros, Geometria Plana, Prismas, Geometria Espacial, Poliedros
Nesta figura, estão representados o cubo ABCDEFGH e o sólido OPQRST:
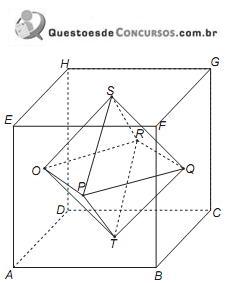
Cada aresta do cubo mede 4 cm e os vértices do sólido OPQRST são os pontos centrais das faces do cubo.
Então, é CORRETO afirmar que a área lateral total do sólido OPQRST mede
Nesta figura, estão representados o cubo ABCDEFGH e o sólido OPQRST:

Cada aresta do cubo mede 4 cm e os vértices do sólido OPQRST são os pontos centrais das faces do cubo.
Então, é CORRETO afirmar que a área lateral total do sólido OPQRST mede

Cada aresta do cubo mede 4 cm e os vértices do sólido OPQRST são os pontos centrais das faces do cubo.
Então, é CORRETO afirmar que a área lateral total do sólido OPQRST mede
A
8√2 cm² .
B
8√3 cm² .
C
16√2 cm² .
D
16√3 cm² .


 ≅ 3, a massa aproximada do porta-joias, em gramas, é
≅ 3, a massa aproximada do porta-joias, em gramas, é




 . Determine a capacidade da cisterna.
. Determine a capacidade da cisterna.