Questõessobre Prismas

InícioTodas as questões
1
1
Foram encontradas 89 questões
0fec501e-04
FGV 2020 - Matemática - Prismas, Geometria Espacial

A figura mostra um sólido composto por 30 cubos idênticos. Quando os cubos destacados em cinza são retirados, a área total do sólido aumenta em 144 cm².



O volume do sólido original, sem a retirada dos cubos destacados em cinza, é igual a

A
1 920 cm³. 
B
2 733,75 cm³.
C
3 750 cm³.
D
4 991,25 cm³
E
6 480 cm³.
a8833898-02
UEG 2017 - Matemática - Prismas, Geometria Espacial

Um porta-canetas tem o formato de um prisma reto de base octogonal, seccionado transversalmente por um plano, conforme indica a Figura 1. A altura maior é 5/4 da altura menor h e a base possui lado medindo a, com altura sendo o dobro do tamanho do lado, conforme a Figura 2.



O volume para esse objeto pode ser descrito pela equação

A
V = 4a² h
B
V = 16a² / h³
C
V = 8a² + 4h / h³
D
V = 4 (a + h)² / h³
E
V = 8ah²
ad6c698a-fa
FASEH 2019, FASEH 2019 - Matemática - Prismas, Geometria Espacial

Um prisma quadrangular regular possui área total de 288 dm² ; se a aresta da base é 2/3 da altura, então, o volume deste prisma, em litros, é:

A
216
B
324
C
2.160
D
2.592
217b831a-f7
UEG 2015 - Matemática - Prismas, Geometria Espacial

Alterando-se as dimensões de uma caixa retangular de altura h, as dimensões da base serão multiplicadas por k e as da altura somado k, em que k é uma constante positiva e não nula. Logo, verifica-se que o volume da nova caixa será em relação à anterior

A
k3 vezes maior
B
k2 + kh vezes maior
C

k2 + vezes maior

D

k3 + vezes maior

aeed9f6b-00
UDESC 2019 - Matemática - Áreas e Perímetros, Geometria Plana, Prismas, Geometria Espacial

Considere um prisma cuja base é um hexágono regular e as faces laterais são quadrados. Se o seu volume for 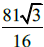cm³, então sua área superficial total é de aproximadamente:

A
13 cm²
B
19 cm²
C
25 cm²
D
15 cm²
E
30 cm²
9f7e260d-5f
ENEM 2020 - Matemática - Prismas, Geometria Espacial

Um clube deseja produzir miniaturas em escala do troféu que ganhou no último campeonato. O troféu está representado na Figura 1 e é composto por uma base em formato de um paralelepípedo reto-retângulo de madeira, sobre a qual estão fixadas três hastes verticais que sustentam uma esfera de 30 cm de diâmetro, que fica centralizada sobre a base de madeira. O troféu tem 100 cm de altura, incluída sua base.


A miniatura desse troféu deverá ser instalada no interior de uma caixa de vidro, em formato de paralelepípedo reto-retângulo, cujas dimensões internas de sua base estão indicadas na Figura 2, de modo que a base do troféu seja colada na base da caixa e distante das paredes laterais da caixa de vidro em pelo menos 1 cm. Deve ainda haver uma distância de exatos 2 cm entre o topo da esfera e a tampa dessa caixa de vidro. Nessas condições deseja-se fazer a maior miniatura possível.

A medida da altura, em centímetro, dessa caixa de vidro deverá ser igual a

A
12.
B
14.
C
16.
D
18.
E
20.
9f51fe1e-5f
ENEM 2020 - Matemática - Prismas, Geometria Espacial

    Num recipiente com a forma de paralelepípedo reto-retângulo, colocou-se água até a altura de 8 cm e um objeto, que ficou flutuando na superfície da água.
    Para retirar o objeto de dentro do recipiente, a altura da coluna de água deve ser de, pelo menos, 15 cm. Para a coluna de água chegar até essa altura, é necessário colocar dentro do recipiente bolinhas de volume igual a 6 cm3 cada, que ficarão totalmente submersas.


O número mínimo de bolinhas necessárias para que se possa retirar o objeto que flutua na água, seguindo as instruções dadas, é de

A
14.
B
16.
C
18.
D
30.
E
34.
9f3ed925-5f
ENEM 2020 - Matemática - Prismas, Geometria Espacial

Em um jogo desenvolvido para uso no computador, objetos tridimensionais vão descendo do alto da tela até alcançarem o plano da base. O usuário pode mover ou girar cada objeto durante sua descida para posicioná-lo convenientemente no plano horizontal. Um desses objetos é formado pela justaposição de quatro cubos idênticos, formando assim um sólido rígido, como ilustrado na figura.


Para facilitar a movimentação do objeto pelo usuário, o programa projeta ortogonalmente esse sólido em três planos quadriculados perpendiculares entre si, durante sua descida.

A figura que apresenta uma possível posição desse sólido, com suas respectivas projeções ortogonais sobre os três planos citados, durante sua descida é

A

B

C

D

E

9efd6469-5f
ENEM 2020 - Matemática - Prismas, Geometria Espacial

Pergolado é o nome que se dá a um tipo de cobertura projetada por arquitetos, comumente em praças e jardins, para criar um ambiente para pessoas ou plantas, no qual há uma quebra da quantidade de luz, dependendo da posição do sol. É feito como um estrado de vigas iguais, postas paralelas e perfeitamente em fila, como ilustra a figura.


Um arquiteto projeta um pergolado com vãos de 30 cm de distância entre suas vigas, de modo que, no solstício de verão, a trajetória do sol durante o dia seja realizada num plano perpendicular à direção das vigas, e que o sol da tarde, no momento em que seus raios fizerem 30° com a posição a pino, gere a metade da luz que passa no pergolado ao meio-dia.
Para atender à proposta do projeto elaborado pelo arquiteto, as vigas do pergolado devem ser construídas de maneira que a altura, em centímetro, seja a mais próxima possível de

A
9.
B
15.
C
26.
D
52.
E
60.
9eecbf69-5f
ENEM 2020 - Matemática - Prismas, Geometria Espacial

    Um processo de aeração, que consiste na introdução de ar num líquido, acontece do seguinte modo: uma bomba B retira o líquido de um tanque T1 e o faz passar pelo aerador A1, que aumenta o volume do líquido em 15%, e em seguida pelo aerador A2, ganhando novo aumento de volume de 10%. Ao final, ele fica armazenado num tanque T2, de acordo com a figura.


    Os tanques T1 e T2 são prismas retos de bases retangulares, sendo que a base de T1 tem comprimento c e largura L, e a base de T2 tem comprimento c/2 e largura 2L.

Para finalizar o processo de aeração sem derramamento do líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido que já saiu de T1, denotada por x, e a altura da coluna de líquido que chegou a T2, denotada por y.

Disponível em: www.dec.ufcg.edu.br. Acesso em: 21 abr. 2015.

A equação que relaciona as medidas das alturas y e x é dada por

A
y = 1,265x
B
y = 1,250x
C
y = 1,150x
D
y = 1,125x
E
y = x
ad8dba71-fd
ENCCEJA 2018 - Matemática - Pirâmides, Prismas, Geometria Espacial

Um arquiteto recebeu uma encomenda para projetar um novo edifício empresarial em uma grande capital brasileira. O cliente, dono do empreendimento, solicitou o projeto de um edifício com a forma de um sólido geométrico, com duas faces paralelas triangulares e faces laterais retangulares.

Atendendo à solicitação do cliente, o edifício a ser projetado pelo arquiteto terá a forma de um(a)

A
pirâmide retangular.
B
pirâmide triangular.
C
prisma retangular.
D
prisma triangular.
be1036de-ff
UNICENTRO 2017 - Matemática - Pirâmides, Prismas, Geometria Espacial, Poliedros

Das afirmações abaixo, assinale a única que está INCORRETA.

A
O cubo é um poliedro que tem 6 faces, 8 vértices e 12 arestas.
B
O prisma é um poliedro porque é um solido cuja superfície é formada por polígonos e seus interiores.
C
Um prisma recebe denominação de acordo com o polígono da base: se a base é um triangulo, o prisma é triangular; se a base é um quadrilátero, o prisma é quadrangular.
D
Uma pirâmide de base octogonal tem 8 arestas, 6 faces e 6 vértices.
f1e26eff-f9
PUC - SP 2017 - Matemática - Prismas, Geometria Espacial

• Um bloco maciço de madeira na forma de um prisma reto de base retangular medindo 18 cm por 24 cm e com 30 cm de altura, foi totalmente dividido em cubinhos iguais e de maior aresta possível. Supondo que não tenha ocorrido perda alguma no corte do bloco, o volume de um cubinho é

A
64 cm3 .
B
125 cm3 .
C
216 cm3 .
D
343 cm3 .
ae274af5-fd
UECE 2019 - Matemática - Prismas, Geometria Espacial

Em um prisma triangular reto, a base XYZ é um triângulo retângulo cuja medida dos catetos são respectivamente 3 m e 4 m. Se a medida do volume desse prisma é 18 m3, então, a medida, em metros quadrados, da superfície total desse prisma é

A
36.
B
48.
C
32.
D
52.
6bee868d-fc
ENCCEJA 2018 - Matemática - Pirâmides, Prismas, Geometria Espacial

Durante uma feira de matemática em uma escola, os alunos resolveram oferecer lembrancinhas em forma de sólidos geométricos. Foram disponibilizados, para a confecção das lembrancinhas, moldes planificados nos formatos representados nas figuras.



Os sólidos que correspondem às planificações apresentadas, respectivamente, nas figuras 1, 2 e 3 são

A
pirâmide de base triangular, cubo e prisma de base triangular.
B
prisma de base triangular, prisma de base hexagonal e pirâmide de base triangular.
C
pirâmide de base triangular, prisma de base hexagonal e prisma de base triangular.
D
prisma de base triangular, cubo e prisma de base pentagonal.
dd8464a1-d8
IF-TO 2016 - Matemática - Prismas, Geometria Espacial

O volume de um prisma é calculado pelo produto de sua base pela altura. Diminuindo 15% de sua base e aumentando 25% de sua altura, esse prisma tem:

A
Um aumento de 20% do seu volume.
B
Um aumento de 6,25% do seu volume.
C
Uma diminuição de 10% do seu volume.
D
Uma diminuição de 12,50% do seu volume.
E
O mesmo volume.
abca1ac2-b3
IF-PR 2016 - Matemática - Prismas, Geometria Espacial

Uma artesã adquiriu um bloco de concreto celular no formato de um prisma retangular de dimensões a = 10cm, b = 30cm e c = 50cm. Ela pretende separá-lo em dois cubos de mesmo volume e, quatro das faces de cada cubo pertencentes às faces laterais do prisma. A medida da aresta ( ℓ ) destes cubos, em cm, pertence ao intervalo:

A

B

C

D

ebcf11c3-dc
FAMEMA 2017 - Matemática - Prismas, Geometria Espacial

A medida da aresta da base quadrada de um prisma reto é igual à medida do diâmetro da base de um cone reto. A altura do prisma é 5,5 cm maior que a altura do cone e o volume do cone é 1/6 do volume do prisma. Considerando π = 3,1, é correto afirmar que a altura do prisma é

A
13,5 cm.
B
18,0 cm.
C
8,5 cm.
D
10,0 cm.
E
15,5 cm.
f427e38c-e9
ULBRA 2011 - Matemática - Prismas, Geometria Espacial, Cilindro

O princípio de Cavalieri permite afirmar que um cilindro e um prisma, com áreas das bases equivalentes e mesma altura, possuem o mesmo volume. Uma empresa, preocupada com o meio ambiente, resolve rever as suas embalagens, com o objetivo de economizar matéria prima. Entre o cilindro de raio 3 cm e altura de 10 cm ou o prisma quadrangular de aresta da base 5,32 cm e altura de 10 cm, ela deve optar pelo:

A
Cilindro, pois são necessários aproximadamente 245 cm² de alumínio para fabricá-lo.
B
Prisma, pois são necessários aproximadamente 200 cm² de alumínio para fabricá-lo.
C
Prisma, pois são necessários aproximadamente 270 cm² de alumínio para fabricá-lo.
D
Cilindro, pois são necessários aproximadamente 145 cm² de alumínio para fabricá-lo.
E
Prisma, pois são necessários aproximadamente 214 cm² de alumínio para fabricá-lo.
671c5363-d8
FAMEMA 2019 - Matemática - Prismas, Geometria Espacial

Um recipiente transparente possui o formato de um prisma reto de altura 15 cm e base quadrada, cujo lado mede 6 cm. Esse recipiente está sobre uma mesa com tampo horizontal e contém água até a altura de 10 cm, conforme a figura.

Se o recipiente for virado e apoiado na mesa sobre uma de suas faces não quadradas, a altura da água dentro dele passará a ser de

A
4 cm.
B
3,5 cm.
C
3 cm.
D
2,5 cm.
E
2 cm.