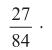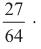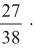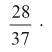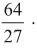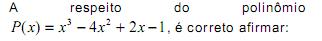9ae26cd9-35
UNESP 2014 - Matemática - Polinômios
O polinômio P(x) = a · x3 + 2 · x + b é divisível por x – 2 e,quando divisível por x + 3, deixa resto – 45. Nessas condições,
os valores de a e b, respectivamente, são
O polinômio P(x) = a · x3 + 2 · x + b é divisível por x – 2 e,quando divisível por x + 3, deixa resto – 45. Nessas condições,
os valores de a e b, respectivamente, são
A
1 e 4.
B
1 e 12.
C
–1 e 12.
D
2 e 16.
E
1 e –12.
 possui assíntotas horizontal e vertical.
possui assíntotas horizontal e vertical.