Questõessobre Polígonos
Considerando C1 a circunferência de centro em um ponto
O e raio r cm; considerando o retângulo ABCD, inscrito
em C1, de modo que o ângulo AÔB meça 150°;
considerando o losango MNPQ cujos vértices são pontos
médios dos lados do retângulo ABCD e considerando a
circunferência C2 inscrita no losango MNPQ, assinale o
que for correto.
A medida do maior lado do retângulo ABCD é maior
do que 2r cm.
Considerando C1 a circunferência de centro em um ponto
O e raio r cm; considerando o retângulo ABCD, inscrito
em C1, de modo que o ângulo AÔB meça 150°;
considerando o losango MNPQ cujos vértices são pontos
médios dos lados do retângulo ABCD e considerando a
circunferência C2 inscrita no losango MNPQ, assinale o
que for correto.
A medida do maior lado do retângulo ABCD é maior
do que 2r cm.
Seja n o número de lados de um polígono convexo P.
Sabendo-se que a soma de n – 1 ângulos internos de P, é 2004º , é correto afirmar que o
número n de lados de P é
O número de polígonos convexos distintos que podemos formar, com vértices
nos pontos de coordenadas (0, 0), (0, 1), (0, 2), (0, 3), (2, 0), (2, 1), (2, 2) e (2, 3),
do plano, é
A partir de uma folha de papel quadrada ABCD , fez-se uma sequência de dobraduras conforme descrito:

Com base nas informações acima, ASSINALE a alternativa INCORRETA.
A partir de uma folha de papel quadrada ABCD , fez-se uma sequência de dobraduras conforme descrito:

Com base nas informações acima, ASSINALE a alternativa INCORRETA.
Um rótulo de forma retangular (figura 1) será colado em toda a
superfície lateral de um recipiente com a forma de um prisma
hexagonal regular (figura 2), sem haver superposição.

Considerando √3 ≅ 1,73, é correto afirmar que a capacidade
desse recipiente é, em mL, aproximadamente,

Considere o quadrilátero ABCD, com A(1, 4), B(5, 1), C(11, 6)
e P(6, 5), sendo P a intersecção das diagonais  A reta r é paralela à diagonal
A reta r é paralela à diagonal  e passa pelo ponto D,
conforme mostra a figura.
e passa pelo ponto D,
conforme mostra a figura. Sabendo-se que P é o ponto médio das diagonais
Sabendo-se que P é o ponto médio das diagonais  a equação da reta r pode ser dada por:
a equação da reta r pode ser dada por:
 A reta r é paralela à diagonal
A reta r é paralela à diagonal 
 a equação da reta r pode ser dada por:
a equação da reta r pode ser dada por: DA PERSPECTIVA DAS AVES: A FASCINANTE GEOMETRIA DA NOVA YORK VISTA DO CÉU
O fotógrafo americano Jeffrey Milstein é conhecido por suas imagens aéreas de cidades e bairros residenciais feitas a
partir de helicóptero. Em seu mais recente projeto, Milstein foi para o céu acima de Nova York
 "É longe o bastante para que a geometria da paisagem urbana, invisível quando vista do chão, apareça em padrões
surpreendentes e, frequentemente, elegantes", acrescentou.
"É longe o bastante para que a geometria da paisagem urbana, invisível quando vista do chão, apareça em padrões
surpreendentes e, frequentemente, elegantes", acrescentou.
Disponível em: http://www1.folha.uol.com.br/bbc/2015/07/1655944‐da‐perspectiva‐das‐aves‐a‐fascinante‐geometria‐da‐nova‐york‐vista‐do‐ceu.shtml. Acesso em 11.10.15
Os tetos dos edifícios da foto aérea feita por Milstein revelam um padrão geométrico peculiar. A maioria dos edifícios
mostrados apresenta dois pares de “saliências laterais”, mas também há alguns com três pares. Os tetos de todos eles
podem ser associados a um polígono não convexo com certo número de lados. Por exemplo, para dois pares de
“saliências laterais”, o polígono do teto tem 20 lados. Se generalizássemos esse padrão considerando um edifício com
݊ pares de “saliências laterais”, o polígono associado ao teto desse edifício teria um número de lados igual a

Na figura, os raios das circunferências
de centros M e N são, respectivamente,
2r e 5r. Se a área do quadrilátero AMBN
é 16√6, o valor de r é


Unindo-se os pontos médios dos lados de um hexágono regular H1, obtém-se
um hexágono regular H2. A razão entre as áreas de H1 e H2 é
João pode ter obtido a situação utilizando quatro
cargas de mesmo módulo e dispondo-as sobre os
vértices de um losango cujo ângulo interno do qual A
é vértice mede 120 graus.
No caso em que o quadrilátero em questão é um
quadrado, o módulo da carga situada sobre o vértice
C (oposto a A) deve ser, necessariamente, o dobro do
módulo da carga que ocupa o vértice B.
Se João colocou nos vértices adjacentes a A cargas de
mesmo módulo, e tais vértices equidistam de A, então
o quadrilátero formado é, necessariamente, um
trapézio.
Uma linha poligonal é construída em etapas. A
primeira etapa é tomar um segmento de
tamanho 1. A segunda etapa consiste em
inserir um triângulo equilátero no terço médio
do segmento e retirar o lado do triângulo que
sobrepõe o segmento da etapa anterior,
conforme figura abaixo. Na terceira etapa,
inserem-se dois triângulos equiláteros nos
terços médios dos segmentos à esquerda e à
direita do triângulo da etapa anterior e retiramse os lados que sobrepõem o segmento da
primeira etapa. Em uma etapa qualquer,
inserem-se triângulos equiláteros nos terços
médios dos segmentos à esquerda e à direita
dos triângulos da etapa anterior e retiram-se os
lados que sobrepõem o segmento da etapa
inicial.

Assinale a alternativa que completa
corretamente a frase abaixo.
Prosseguindo a construção da linha poligonal
desta maneira, o comprimento da linha
poligonal

A figura indica a medida de alguns dos ângulos internos de
um quadrilátero ABCD e de um triângulo ADE, sendo que AE é paralelo a CD.

Nessa situação, a medida do ângulo CDA, indicada por z,
é igual a

Observe as três primeiras linhas de um padrão, que continua
nas linhas subsequentes.

Na 30a
linha desse padrão, o maior número da soma em
vermelho, indicada dentro do retângulo, será igual a

O quadrilátero ABCD indicado na figura possui ângulo reto em A, um ângulo externo de 60° em B e três lados de medidas conhecidas que são AB = 7cm, BC = 6cm e C = 12cm.

Nesse quadrilátero, a medida de 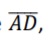 em centímetros, é
igual a
em centímetros, é
igual a
O quadrilátero ABCD indicado na figura possui ângulo reto em A, um ângulo externo de 60° em B e três lados de medidas conhecidas que são AB = 7cm, BC = 6cm e C = 12cm.

Nesse quadrilátero, a medida de 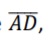 em centímetros, é
igual a
em centímetros, é
igual a
A figura, feita em escala, indica um painel formado por sete
retângulos amarelos idênticos e dois retângulos azuis idênticos. Cada retângulo azul tem dimensões x e y, ambas em
metros.

Na situação descrita, x – y é igual a

Dois lados consecutivos de um
paralelogramo medem 6 e 8 e uma de suas
diagonais mede 2√13. Se d é a medida da
outra diagonal, podemos afirmar que:
Na figura a seguir, AD mede 12 cm, BD mede 4 cm, BC mede 12 cm, o ângulo B mede 90º
e DE é paralelo a BC.

Ao rotacionarmos o trapézio BCED em torno do lado BD, produzimos um tronco de cone cujo volume é
