4c9792b4-e4
UCB 2012 - Matemática - Geometria Espacial, Poliedros
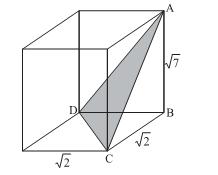
Considere um cubo ABCDEFGH no qual ABCD é uma face com 16 cm2 de área, AE e BH são arestas e AG é uma diagonal do cubo.
No cubo citado, toma-se um plano secante cujas interseções com as arestas AB, BC, CG, FG, EF e AE se dão exatamente nos pontos médios dessas arestas. Considere √3 = 1,7 e calcule, em centímetros quadrados, a área da região de interseção entre o plano e o cubo. Marque na folha de respostas, desprezando, se houver, a parte decimal do resultado final.
Gabarito Tipo B
Considere um cubo ABCDEFGH no qual ABCD é uma face com 16 cm2 de área, AE e BH são arestas e AG é uma diagonal do cubo.
No cubo citado, toma-se um plano secante cujas interseções com as arestas AB, BC, CG, FG, EF e AE se dão exatamente nos pontos médios dessas arestas. Considere √3 = 1,7 e calcule, em centímetros quadrados, a área da região de interseção entre o plano e o cubo. Marque na folha de respostas, desprezando, se houver, a parte decimal do resultado final.
Gabarito Tipo B
No cubo citado, toma-se um plano secante cujas interseções com as arestas AB, BC, CG, FG, EF e AE se dão exatamente nos pontos médios dessas arestas. Considere √3 = 1,7 e calcule, em centímetros quadrados, a área da região de interseção entre o plano e o cubo. Marque na folha de respostas, desprezando, se houver, a parte decimal do resultado final.
Gabarito Tipo B
C
Certo
E
Errado



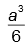
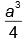
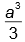
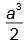
 , a aréa
, a aréa 