c13d90ad-1c
PUC - SP 2015 - Matemática - Números Complexos
Se 2 é a única raiz real da equação x3 – 4x2 + 6x – 4 = 0, então, relativamente às demais
raízes dessa equação, é verdade que são números
complexos
Se 2 é a única raiz real da equação x3 – 4x2 + 6x – 4 = 0, então, relativamente às demais
raízes dessa equação, é verdade que são números
complexos
A
cujas imagens pertencem ao primeiro e quarto
quadrantes do plano complexo.
B
que têm módulos iguais a 2.
C
cujos argumentos principais são 45° e 135°.
D
cuja soma é igual a 2i.
 , onde
, onde 


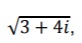 onde i é a unidade imaginária. O valor de xy é igual a
onde i é a unidade imaginária. O valor de xy é igual a = 0, em que
= 0, em que  = x – yi e = y – xi, então o valor da soma |x| + |y| é
= x – yi e = y – xi, então o valor da soma |x| + |y| é  considerando o argumento principal, é
considerando o argumento principal, é 





 + ai, onde a é um número real positivo, representam no plano complexo vér- tices de um triângulo eqüilátero. Dado que
+ ai, onde a é um número real positivo, representam no plano complexo vér- tices de um triângulo eqüilátero. Dado que  o valor de a é:
o valor de a é:






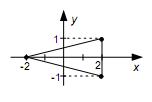
 é o número complexo conjugado de z, então as únicas soluções da equação
é o número complexo conjugado de z, então as únicas soluções da equação 

 são pontos do plano complexo, então
são pontos do plano complexo, então  encontra-se no primeiro quadrante desse plano
encontra-se no primeiro quadrante desse plano