Qual região foi selecionada para o investimento da
construtora?


Considere a matriz  , onde x e y
são números reais. Se M2 = M.M, então, o
determinante de M2 é igual a
, onde x e y
são números reais. Se M2 = M.M, então, o
determinante de M2 é igual a

Considerando-se as matrizes  e Z = (2X).Y, é correto afirmar que o
determinante da matriz Z é igual a
e Z = (2X).Y, é correto afirmar que o
determinante da matriz Z é igual a







Dadas as matrizes 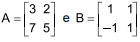 , o determinante de (AB + At
), em que At
é a transposta da matriz A, é igual a
, o determinante de (AB + At
), em que At
é a transposta da matriz A, é igual a
Se M é a matriz M =  e det(M) é o determinante de M, então, para um
número inteiro k, todas as soluções x da equação
det(M) = 0 são da forma
e det(M) é o determinante de M, então, para um
número inteiro k, todas as soluções x da equação
det(M) = 0 são da forma
Considere as matrizes reais M =  e
N =
e
N =  Se o determinante de M é igual a 2 e
o determinante de N é igual a 1, então, o produto
a.b pode ser igual a
Se o determinante de M é igual a 2 e
o determinante de N é igual a 1, então, o produto
a.b pode ser igual a
 , o valor de
2a + √2b
é
, o valor de
2a + √2b
éSejam  uma matriz e A−1 = (bij)3×3 a inversa de
A. O valor de b11 + b22 + b33 é:
uma matriz e A−1 = (bij)3×3 a inversa de
A. O valor de b11 + b22 + b33 é:
Qual foi o par de letras que, após a criptografia, se tornou  ?
?
Leia atentamente as instruções abaixo e responda à questão:
Podemos criptografar mensagens, utilizando operações matriciais da seguinte maneira:
• Cada letra do alfabeto está associada a um único número, conforme tabela abaixo.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
• A fim de montarmos uma matriz quadrada 2 x 2 ou 3 x 3, determinamos se vamos criptografar de 2 em2 letras ou de 3 em 3 letras.
• Para obter uma nova matriz com dados criptografados, multiplicamos a matriz quadrada por uma matriz coluna (formada pelos números que representam as letras).
Suponhamos que desejamos transmitir a seguinte mensagem: “Olá pessoal, tudo ok, cheguei atempo de fazer a prova do vestibular do UniFOA”. Para tanto, vamos utilizar a matriz  que criptografará cada par de letras da mensagem. Ao criptografar um par de letras da mensagem com a seguinte operação matricial
que criptografará cada par de letras da mensagem. Ao criptografar um par de letras da mensagem com a seguinte operação matricial  , obtemos o novo par
, obtemos o novo par  .
.
 , realizando a seguinte operação matricial:
, realizando a seguinte operação matricial:Leia atentamente as instruções abaixo e responda à questão:
Podemos criptografar mensagens, utilizando operações matriciais da seguinte maneira:
• Cada letra do alfabeto está associada a um único número, conforme tabela abaixo.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
• A fim de montarmos uma matriz quadrada 2 x 2 ou 3 x 3, determinamos se vamos criptografar de 2 em2 letras ou de 3 em 3 letras.
• Para obter uma nova matriz com dados criptografados, multiplicamos a matriz quadrada por uma matriz coluna (formada pelos números que representam as letras).
Suponhamos que desejamos transmitir a seguinte mensagem: “Olá pessoal, tudo ok, cheguei atempo de fazer a prova do vestibular do UniFOA”. Para tanto, vamos utilizar a matriz  que criptografará cada par de letras da mensagem. Ao criptografar um par de letras da mensagem com a seguinte operação matricial
que criptografará cada par de letras da mensagem. Ao criptografar um par de letras da mensagem com a seguinte operação matricial  , obtemos o novo par
, obtemos o novo par  .
.
Se θ = π/8 radianos e A =  , então o determinante de A9 é igual a
, então o determinante de A9 é igual a
1/16√2
1/32√2
Se  então
det(A) + det(A2)+ det(A3) + ⋯ + det(A100),
onde
então
det(A) + det(A2)+ det(A3) + ⋯ + det(A100),
onde  , vale:
, vale:
100100
Dadas as matrizes,  e,
e,  tal que A ∙ B = C é:
tal que A ∙ B = C é:
 , tal que
, tal que  , os valores de x, y e z, são, respectivamente:
, os valores de x, y e z, são, respectivamente:  , logo a mensagem recebida é amor.
, logo a mensagem recebida é amor.
 , então a matriz A é
, então a matriz A é


